[DSP 01] LTI System
LTI system 이란?
Linear Time-Invariant System, 즉 선형 시불변 시스템이다.
라고 해석만 하면 면접에서 광탈이다.
각각의 개념을 먼저 이해해야 한다. ★ 알고 넘어가자 ★
Time-Invariant System (시불변 시스템)
- 정의 : 시스템의 특성이 시간에 지남에 따라 변하지 않는 시스템
- 즉, 어떤 입력 신호가 Time-shift (시간 지연) 되어 시스템에 입력되었을 때, 원래 출력 신호(지연되지 않은 입력에 대한 출력)가 입력 신호가 지연된 시간만큼 time-shift 된 결과를 출력해낸다면, 그 시스템은 Time-Invariant system 이다. 종종 Shift-Invariant system 이라고도 불린다.
\(\text{s.t. Input } x_1[n] = x[n-n_0] → y_1[n] = y[n-n_0]\) \(\text{where a system transforms the input } x[n] \text{ into the output } y[n]\)
-
예시
1) \(y(t) = \sin x(t)\) 인 시스템에 \(x_1(t)\) 입력을 넣어주면, \(y_1(t) = \sin [x_1(t)]\) 가 나오게 된다.
2) 그럼, 입력 \(x_2(t) = x_1(t-t_0)\) 를 넣어준다면, \(y_2(t) = \sin[x_2(t)]\) \(= \sin [x_1 (t-t_0)] = y_1(t-t_0)\) 을 만족한다.
3) 따라서, 시스템 \(y(t)\) 는 time-invariant 하다.
-
이 외 \(y = tx(t)\) 시스템과, Accumulator 시스템
(\(\text{s.t. }\) \(y[n-n_0] = \sum^{n-n_0}_{k=-\infty} x[k]\) )도 time-invariant 하다.
-
Not time-invarinat 한 시스템으로는 Compressor system이 있는데 \(M\) 이 양의 정수, \(-\infty < n < \infty\)일 때 \(y[n] = x[Mn]\) 인 시스템을 말한다.
Linear System (선형 시스템)
- 입력 신호의 변화에 따라 출력 신호에서도 비례적으로 입력 변화량을 반영하는 시스템
- Superposition Principle (중첩의 원리 - Additivity + Homogeneity)를 만족하는 시스템
- Additivity (가산성)
- 두 연속시간 신호가 더해져서 시스템에 입력되고 이를 통해 얻어진 출력 신호가 두 연속시간 신호를 분리해서 각각 시스템에 입력하고 얻어진 출력 신호를 합친 것과 동일하다.
- 즉, 더해서 넣어서 뺀 거랑, 뺀 거를 더한 거랑 같다는 뜻..–;
- Homogeneity (Scaling - 균일성)
- 연속시간 신호에 임의의 상수 a를 곱합 입력을 시스템에 입력하여 얻어진 출력 신호는 연속시간 신호를 입력하고 출력 신호에 상수 a를 곱한 것과 같다.
LTI 시스템이 중요한 역할을 하는 이유
??? Why LTI?
- 물리적 프로세스들은 LTI 성질을 가지고 있는 경우가 많아서, LTI system 으로 모델링 되는 경우가 많다.
- LTI system 을 통해 신호 및 시스템 분석에 있어 핵심 요소인 LTI properties 와 a set of powerful tools 를 이해할 수 있기 때문에 신호 및 시스템을 상당히 상세하게 분석할 수 있다.
A LTI system is a linear operator defined on a function space that commutes with every time shift operator on that function space. It is particularly easy to calculate the output of a system when an eigenfunction is the input as the output is simply the eigenfunction scaled by the associated eigenvalue.
그럼 어떻게 쓰는가?
- LTI system 에 대한 입력을 basic signal 들의 linear combination의 형태로 나타내준다.
- Superposition 를 이용해서 시스템의 출력을 basic signals 에 대한 response 형태로 계산한다.
- Unit impulse → very general signals can be represented as linear combinations of delayed impulses.
- superposition + time invariance → characterization of any LTI systems in terms of its response to a unit impulse with convolution sum(integral).
그전에 Convolution 연산을 알아봅시다.
Convolution 연산은 어따 쓰는겨?
LTI시스템 상에서 이전값과 현재값을 연산하기 위해
시스템이 메모리가 있는 경우, 시스템의 출력이 현재 입력에 의해서만 결정되는 것이 아닌 이전 입력(causal system 이라면)에 의해서도 영향을 받기 때문에 그에 대한 출력을 나타내기 위해 하는 연산이다.
예를 들어 종(鍾)을 LTI(Liner Time Invariant) 시스템이라고 가정한다면 종을 한번 치면 그 소리가 치는 순간만 나는게 아니라 치는 순간에 소리가 크게 났다가 점점 소리가 감쇄되며 작아진다. 그림으로 나타내면 다음 그림의 첫번째 경우와 같다. 종을 한번 탕 치는 것을 impulse 입력이라 하고 한 번 종을 쳤을 때 나는 소리를 삼각형으로 나타내었다.
그런데 종을 한번 치고 다시 치면 어떨까? 그림의 두번째 경우는 처음 종을 치고 잠시 후 이전보다 약하게 친 경우이다. 이 때는 종소리를 Linear system으로 가정했기 때문에 이전의 입력에 의해 나고 있는 소리에 현재 입력에 의해 나는 소리가 더해져 나타난다. 그리고 이것은 impulse 입력과 종소리의 convolution 과 같은 결과가 나올 것이다.
따라서 convolution은 한 LTI 시스템에 대해 현재와 이전의 입력에 대한 출력을 계산하기 위해 수행하는 것이다.
그림의 두번째 경우를 보면 왜 컨볼루션을 할 때 system이나 입력 중 하나를 반전시켜야 하는지에 대해 알 수 있다.
한 시스템에 시간적으로 앞선 입력을 먼저 넣고 그 후에 시간적으로 나중에 발생한 입력을 넣어야 올바른 출력을 얻을 수 있기 때문에 시간적으로 앞선 입력을 먼저 넣기 위해 입력을 반전시키거나 시스템을 반전시키는 것이다.
입력을 반전시키지 않으면 처음에 종을 약하게 치고 그 후에 세게 친것과 같은 결과가 나오기 때문에 시간적으로 반대의 결과가 나온다.
Reference: https://trip2ee.tistory.com/101
메모리가 있는 선형 시스템 * 임펄스 입력 = 출력 Response
북채 때리는 순간과 내부 공명
https://pulse.embs.org/january-2015/history-convolution-operation/
Convolution 의 특성
- LTI시스템의 인과성
- 현재와 과거에만 의존, 미래 입력을 사용하지 않는 시스템
- h[n]=0, n<0
- impulse response ⇒ h[n]u[n]
- LTI시스템의 안정성
- BIBO(Bounded-Input Bounded-Output)
- 입력 크기가 제한되면 출력 크기도 제한됨
- Conv 연산법칙
- 교환 법칙
- 결합 법칙
- 분배 법칙
- 곱셈 → 샘플링! x[n] delta[n-n_0] = x[n_o] delta[n-n_0]
- 컨벌루션 → 필터 or 지연 x[n]*delta[n-n_0] = x[n-n_o]
- Impulse 의 Conv
- Unit Step signal의 Conv
??? 컨벌루션 연산이 왜 나왔고, 어디서부터 유래가 되었는지?
→ 수학적 도구를 이용하여 해석하고 설계하기 용이하기 때문에, 즉! 컴퓨터를 이용하여 처리하기 쉽다.
→ 임펄스 응답으로부터 임의의 입력 신호에 대한 출력 계산 가능
???? 왜 신호를 complex exponential 로 ?
???? eigenfunction을 왜??
??? 오똫게 eigenfunction으로 복소지수를 찾아냈나?
→ 다 계산하기 편하기 위해서
It is an important and fundamental fact that a sum of sinusoids at the same frequency, but different phase and amplitude, can always be expressed as a single sinusoid at that frequency with some resultant phase and amplitude. An important implication, for example, is that
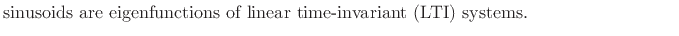
That is, if a sinusoid is input to an LTI system, the output will be a sinusoid at the same frequency, but possibly altered in amplitude and phase. This follows because the output of every LTI system can be expressed as a linear combination of delayed copies of the input signal. In this section, we derive this important result for the general case of sinusoids at the same frequency.
선형 시스템을 통과해도 기본성질이 변화하지않는 신호 = 고유 함수
-
지수함수의 경우에, 지수입력신호에 의한 선형 시스템 출력은, 지수는 같지만 크기(상수배)는 달라짐 즉, A e^at -> B e^at (단지 진폭만 변화할 뿐 같은 지수를 갖음) 대부분의 복소 지수 함수에서, 지수는 주파수 성분을 포함

Leave a comment