[DSP 03] Z-Transform & Discrete-Time LTI System
Z-변환과 이산시간 시불변-선형 시스템
[1] Introduction
- Z-변환Z-Transform은 이산시간Discrete-time(t-domain)의 신호Signals나 시퀀스Sequences, 시스템을 z-domain에 나타내어 분석하는 데에 쓴다.
- 차분 방정식Difference equations을 대수식Algebraic equations으로 변환해주는 이산시간에서의 라플라스 변환Laplace Transform이라고 생각하면 된다.
- 정확하게 말하자면, LCCDELinear Constant-Coefficient Difference Equation를 풀기 위한 것이다.
- 푸리에 변환Fourier Transform은 모든 시퀀스를 수렴시키지는 않는다. 따라서 푸리에 변환을 일반화하고, 신호 및 시스템을 더 표기가 편한 z-변환의 형태로 바꾸어 분석하기 위해 쓰인다.
[2] Definition
-
일반적인 이산시간 신호 $x[n]$에 대해서, 다음과 같이 Infinite sum 또는 Infinite Power series라고 불리는 식으로 정의한다.
\[X(z)= Z\{ x[n]\} = \sum_{n=-\infty }^{\infty}x[n]z^{-n}\]- 엄밀히 말하자면, 위 표현은 양방향Bilateral or Two-sided z-변환으로, 단방향Unilateral 0r Single-sided, one-sided z-변환은 다음과 같다.
- $n<0$에서 $x[n] = 0$ (즉, Causal sequence)이면, 단방향과 양방향 변환이 같다.
- 이 때, $z$는 극좌표Polar form에서 복소 값을 가진Complex-valued 연속 변수이다.
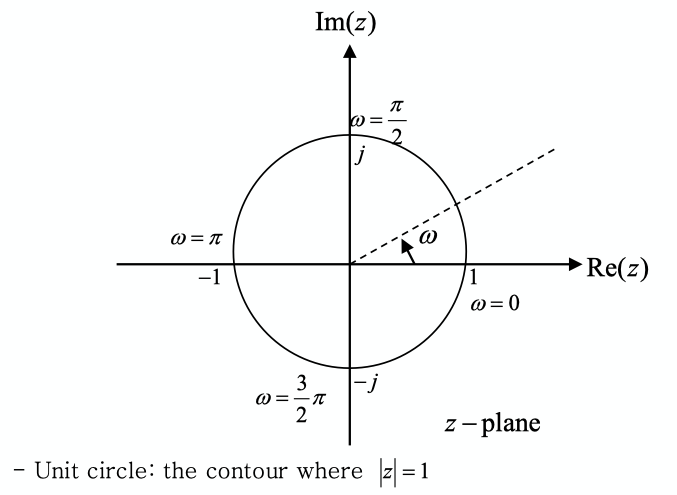
$ω$: $z$의 각도Angle
- 즉, z-변환은 복소함수 이므로, 복소 z-평면을 사용하여 표현하고 해석하기 쉽다.
-
이러한 시퀀스와 z-변환 관계는 다음 처럼 표기한다.
\[x[n] \leftrightarrow X(z)\]
[3] DTFT와 Z-변환의 관계
DTFT는 $r=1$일 때 z-변환이다.
\[X(e^{j\omega})=X(z)|_{z=1\cdot e^{j\omega}} = \sum_{n=-\infty }^{\infty}x[n]e^{-j\omega n}\]- 여기서 $r=1$ 이면 (i.e. $| z | =1$), z-변환은 $x[n]$의 DTFT가 된다.
-
다시 말해, DTFT는 단위 원(Unit circle) $r = 1$ 에서의 z-변환이 된다.
\[z = re^{j\omega}\ (r=1, \ 0 \le \omega \le 2\pi)\]
z-변환은 $x[n]r^{-n}$의 DTFT이다.
\[X(z)=\sum_{n=-\infty }^{\infty}x[n](re^{j\omega})^{-n}=\sum_{n=-\infty }^{\infty}x[n]r^{-n}e^{-j\omega n}\] \[Z\{x[n]\} = DTFT\{x[n]r^{-n}\}\]존재여부 (Existence)
-
(1) $x[n]$가 Absolutely summable하지도 (2) Square-summable하지도 않으면, DTFT는 존재하는지 안하는지 모른다. 하지만 z-변환은 존재한다!
-
(1) Absolutely summable - Stable
- Absolute summability는 DTFT가 존재하기 위한 충분조건이다.
- DTFT가 존재하기 위해선 $| X(e^{jω})| $가 존재해야 한다.
- (2) Square-summable - Finite Energy
- Absolutely summable 하지 않아도, Square-summable 하면 DTFT가 존재한다.
[4] 수렴범위 (ROC: Region of Convergence)
- DTFT와 비슷하게, z-변환도 모든 시퀀스나 $z$ 값에 대해 수렴 하지는 않는다.
- 시퀀스가 absolutely summable하면, DTFT에서는 $ω$에 대한 연속함수로 수렴하게 된다.
- z-변환도 수렴 범위 내에서만 가능하다.
Definition
- z-변환이 수렴할 때, 복소 값 $z$의 집합(또는 값들의 범위), $| z| $에 의해 결정된다.
-
DTFT에서 부터 일반화, z-변환의 정의인 멱급수의 수렴 범위
\[|X(z)|= \left| \sum_{n=-\infty }^{\infty}x[n]z^{-n}\right|\le \sum_{n=-\infty }^{\infty}|x[n]||z^{-n}| \le\sum_{n=-\infty }^{\infty}|x[n]| < \infty\] - e.g. $x[n] = u[n]$
- u[n]은 absolutely summable하지 않아 DTFT가 존재하지 않는다.
- 하지만 $r^{-n}u[n]$은 $r>1$이면 absolutely summable 하여 u[n]에 대한 z-변환은 $r =| z | > 1$일 때 존재한다.
[5] ROC 특징
[6] 주요 z-변환 쌍
| Sequence | Transform | ROC |
|---|---|---|
| 1. $\delta [n]$ | $1$ | All $z$ |
| 2. $u[n]$ | $1\over{1-z^{-1}}$ | $| z | > 1$ |
| 3. $-u[-n-1]$ | $1\over{1-z^{-1}}$ | $| z | < 1$ |
| 4. $\delta [n-m]$ | $z^{-m}$ | All $z$ except $0$ if $m>0$ or $\infty$ if $m<0$ |
| 5. $a^{n}u[n]$ | $1\over{1-az^{-1}}$ | $| z | > | a | $ |
| 6. $-a^{n}u[-n-1]$ | $1\over{1-az^{-1}}$ | $| z | < | a | $ |
| 7. $na^{n}u[n]$ | ${az^{-1}}\over{(1-az^{-1})^2}$ | $| z | > | a | $ |
| 8. $-na^{n}u[-n-1]$ | ${az^{-1}}\over{(1-az^{-1})^2}$ | $| z | < | a | $ |
| 9. $\cos{(\omega_0 n)}u[n]$ | $1-\cos{(\omega_0)}z^{-1}\over{1-2\cos(\omega_0)}z^{-1}+z^{-2}$ | $| z| >1$ |
| 10. $\sin{(\omega_0 n)}u[n]$ | $\sin{(\omega_0)}z^{-1}\over{1-2\cos(\omega_0)}z^{-1}+z^{-2}$ | $| z| <1$ |
| 11. $r^n\cos{(\omega_0 n)}u[n]$ | $1-r\cos{(\omega_0)}z^{-1}\over{1-2r\cos(\omega_0)}z^{-1}+r^2z^{-2}$ | $| z| >r$ |
| 12. $r^n\sin{(\omega_0 n)}u[n]$ | $r\sin{(\omega_0)}z^{-1}\over{1-2r\cos(\omega_0)}z^{-1}+r^2z^{-2}$ | $| z| >r$ |
| 13. $a^n, 0\le n\le N-1\ \ 0$, otherwise | $1-a^Nz^{-N}\over{1-az^{-1}}$ | $| z| >0$ |
Reference
- Alan V. Oppenheim, Discrete-time Signal Processing, Pearson Education
- Hwei Hsu, Schaum’s Outline of Signals and Systems, McGraw-Hill
Leave a comment