[Data Structure] 힙 (Heap)

정의

• Complete Binary Tree^{완전 이진 트리}에 있는 노드 중에서 키 값이 가장 큰 노드나 키 값이 가장 작은 노드를 찾기 위해서 만든 자료구조. 즉, 힙은 반드시 완전 이진트리여야 한다. Priority queue^{우선순위 큐}라고도 불린다.
• 여기서는 Min Heap^{최소 힙}에 대해서 주로 다룰 것이다. Max-heap^최대힙은 본질적으로 같지만 단지 오름차순이 아닌 내림차순일 뿐이다.

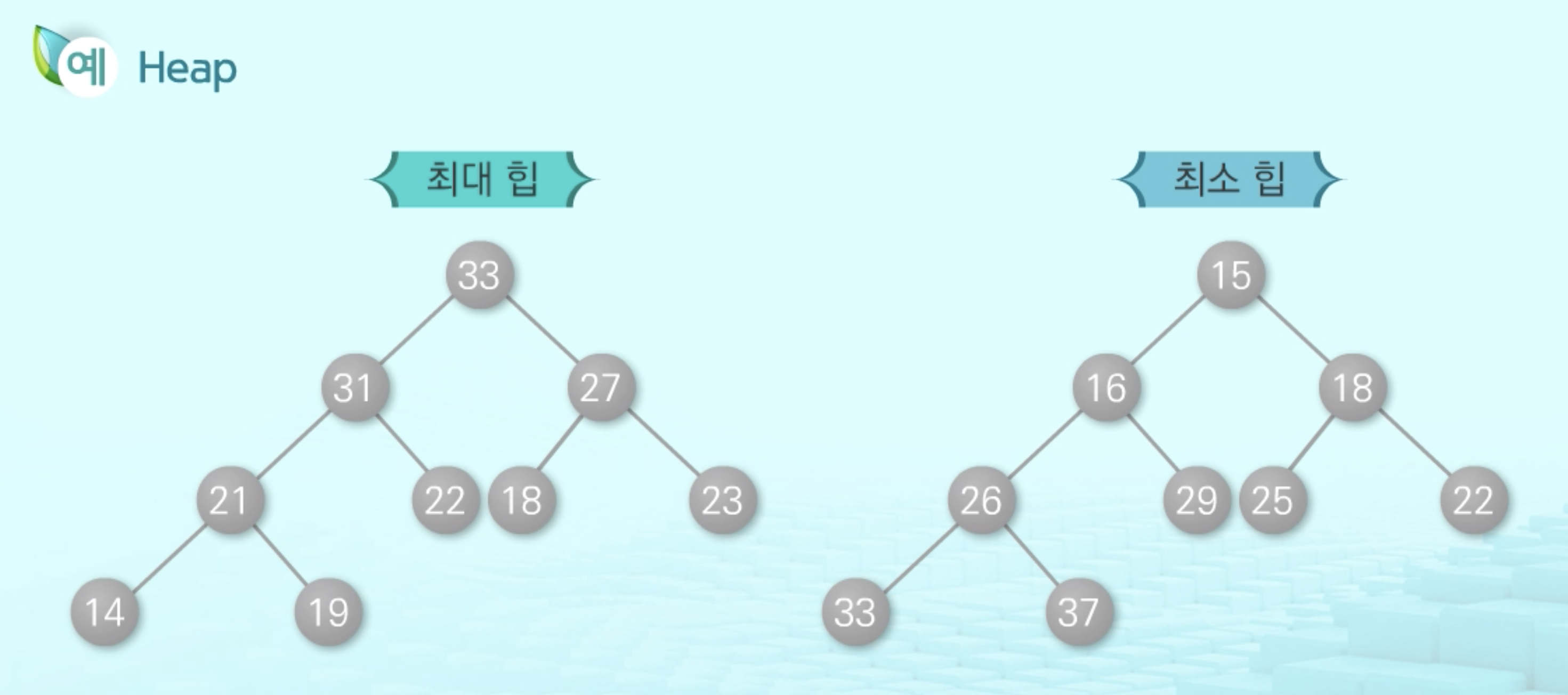
Min Heap (최소 힙)

• 키 값이 가장 작은 노드를 찾기 위한 Complete binary tree(완전 이진 트리)
• 부모 노드의 키 값 < 자식 노드의 키 값
• Root node: 키 값이 가장 작은 노드

Max Heap(최대 힙)

• 키 값이 가장 큰 노드를 찾기 위한 완전 이진 트리
• 부모 노드의 키 값 > 자식 노드의 키 값
• Root node: 키 값이 가장 큰 노드

힙의 연산

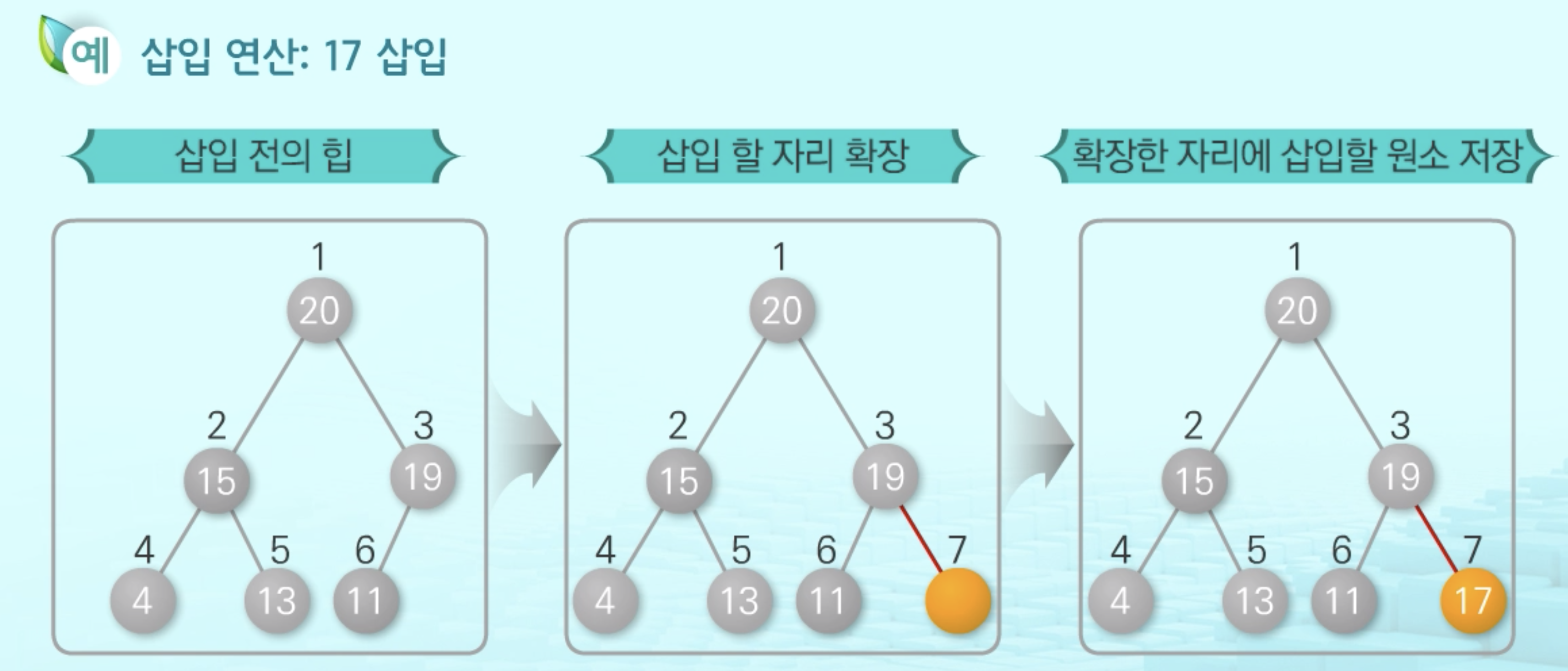
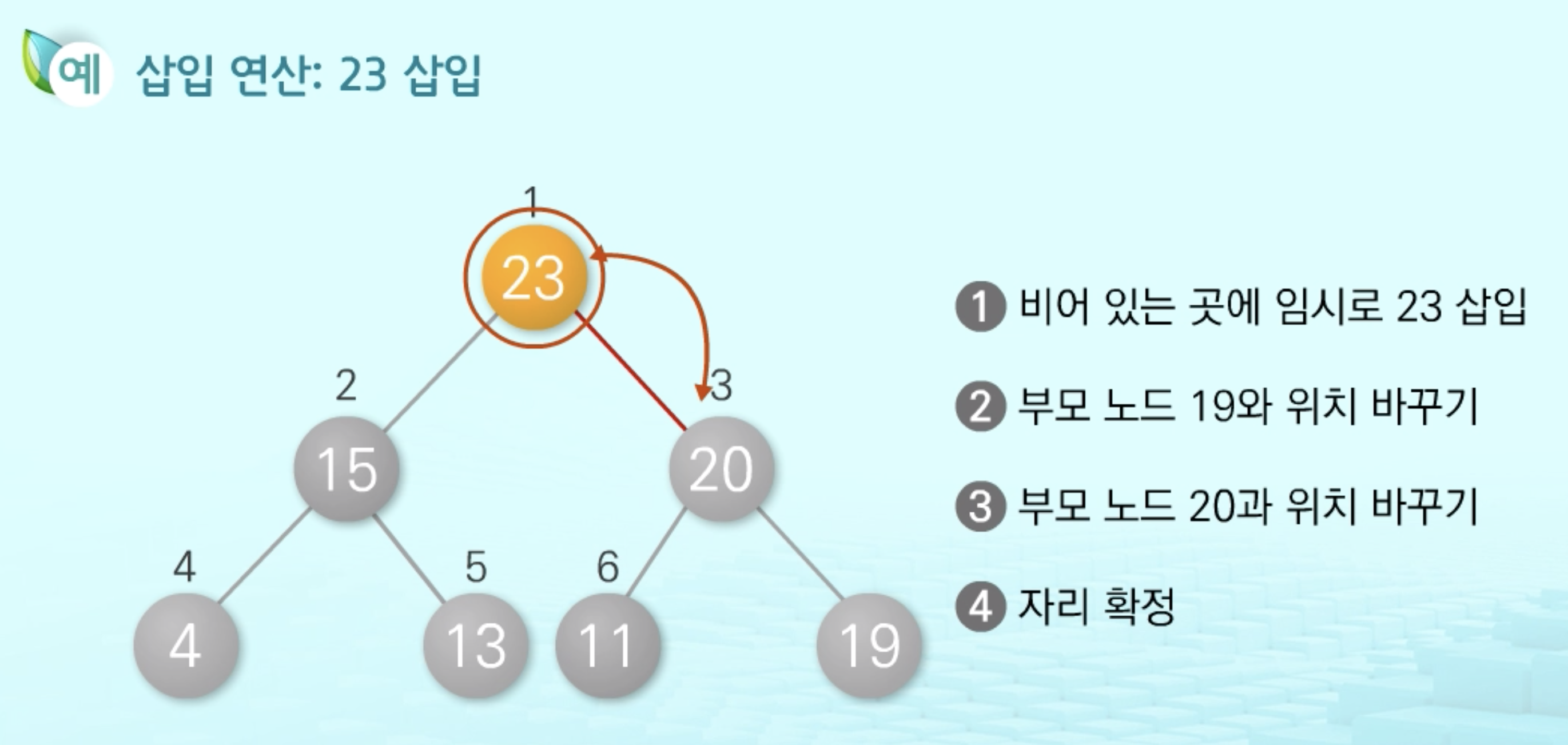
1. 삽입 (O(logN))

• Python에선 heapq.heappush(<heap>, <item>)
• heappush 를 하려면 기존에 heap이 된 상태에서 넣어줘야 한다. 즉, heapify 후에 heappush
• 숫자 하나를 추가하고, 다시 재정렬

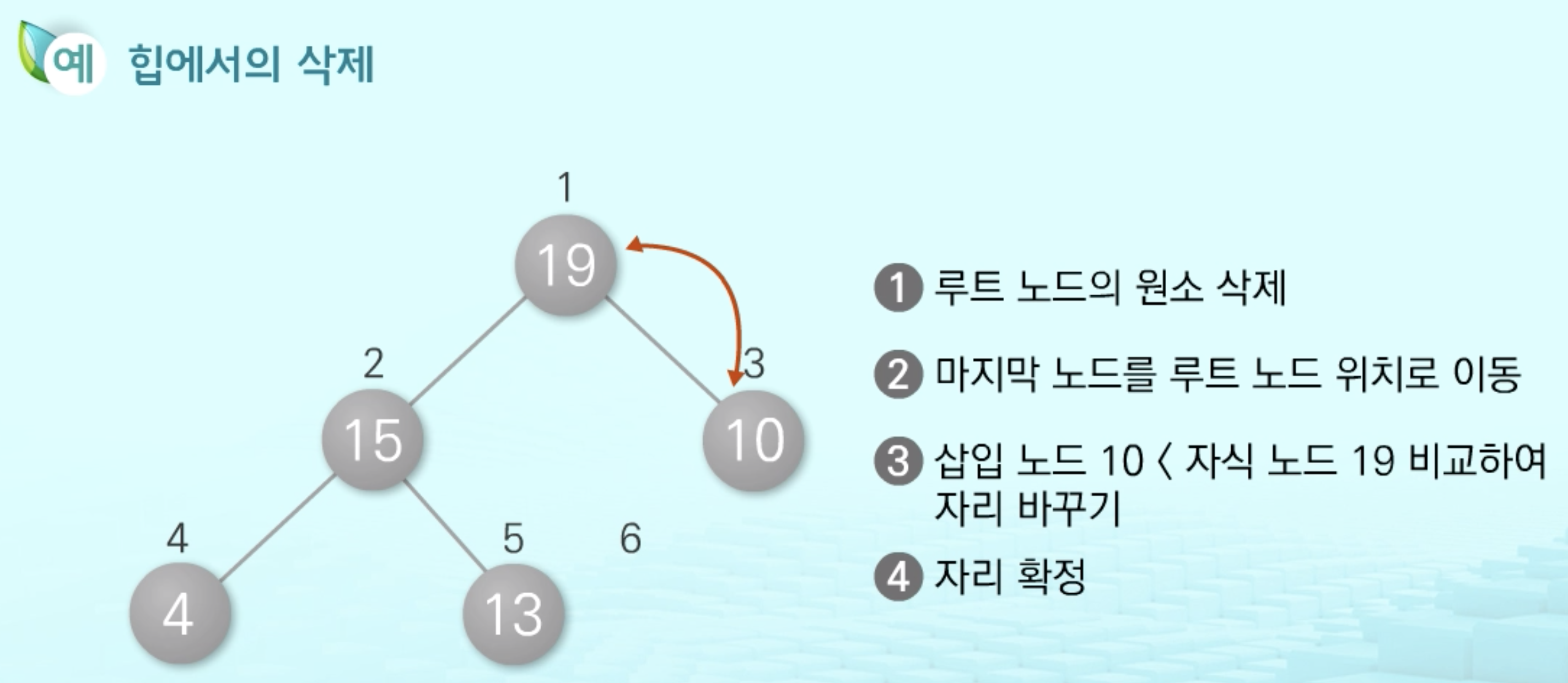
2. 삭제 (O(logN))

• 루트 노드의 원소만 삭제할 수 있음
• 힙의 종류에 따라 최솟값 또는 최댓값을 구할 수 있음. 즉, 우선순위 큐이다.

3. heapify (O(N logN))

• 일반 list를 key를 기준으로 heap화 한다
• heapq.heapify(heap)

응용 : heapq를 최대힙으로 사용하는 방법

• heapq 라이브러리는 기본적으로 최소힙으로 구현되어 있다.
• 만약에 heapq를 간단하게 조작하여 최대 힙으로 사용하고 싶다면, 원소를 음수로 바꾸면 최소 힙에서 최대 힙으로 우선순위가 역전되도록 만들어 사용할 수 있다. (코딩테스트 연습하다 얻은 잡기술)

Reference

• 그림자료들: https://swexpertacademy.com/