[Speech] Conv-TasNet 톺아보기 (1)

9 minute read

들어가며

Conv-TasNet은 2019년도 IEEE/ACM TASLP (Transactions on Audio, speech, and language processing) 저널에 출판된 논문으로, speech separation은 TasNet 이전과 이후로 나뉜다고 말할 수 있을 만큼 이 분야의 역사에 한 획을 그었습니다. 여전히 separation과 enhancement 분야에서 응용되고 있으며, 특히 Conv-TasNet을 기반으로 한 다양한 변형 모델이 나오며 성능향상 (e.g., DPRNN (ICASSP 2020), DPTNet (Interspeech 2020), SepFormer (ICASSP 2021) 등)을 보이고 있어, Conv-TasNet을 읽고, 분석 및 정리해 보았습니다.

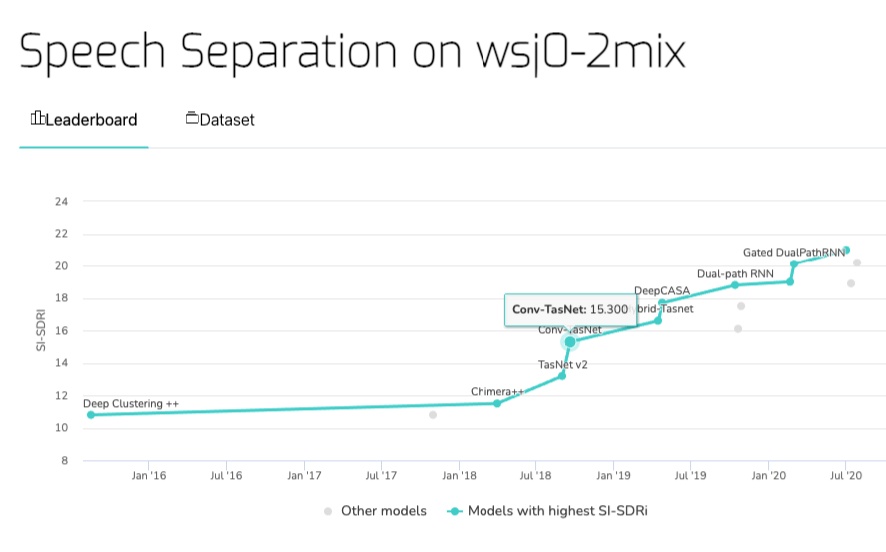
Figure. 1 Speech Separation SOTA Performance on wsj0-2mix
(출처 : Papers with code)

본 글에서는 Conv-TasNet의 전반적인 구조에 대해 다루어 볼 것이고, 다음 글에서는 모델의 encoder/decoder representation에 대한 고찰과 다양한 hyperparameter configuration을 통한 실험으로 도출된 insight에 대해 알아보겠습니다.

TL;DR

Conv-TasNet은 여러 트렌디한 deep learning 테크닉들 (TCN, LN, MobileNet 등)을 가져와 Audio 분야에 잘 조화시킨 End-to-End framework로, 각 speech source에 대한 mask를 time-domain에서 직접 estimation하는 speech seaparation^{음원 분리} 모델이다. 성능적으로도 상당한 breakthrough를 이뤄내었다.
- wsj0-2mix dataset 기준 SI-SNRi 15.3dB, 기존 state-of-the-art 모델에서 4dB에 가까운 성능 향상
Speech separation task에서는 기존 접근 방법처럼 mixture signal을 time-frequency representation (즉, STFT를 통한 spectrogram representation)에서 처리하면 다음과 같은 이유로 suboptimal하기 때문에, time-domain approach로 문제를 해결하였다.
- Spectrogram 계산 시 high-resolution frequency decomposition을 필요로 하기 때문에, 긴 temporal window를 이용해 STFT를 하게 되고, long latency를 야기한다.
- 또한, signal의 phase와 magnitude가 decoupling되기 때문에, clean source들의 phase reconstruction 시 정확도에 upper bound를 야기한다.
Speech waveform을 speech separation task에 optimal한 latent represenatation으로 만들어 End-to-End deep learning framework을 구축하였다.
- Latent representation을 만들어 주는 linear autoencoder는 SI-SNR loss를 최소화 해주도록 separator와 jointly training하였고, 실제 구현 시에는 1-D convolution과 1-D transposed convolution을 이용해 구현하였다.
물론, 다음과 같은 제약이 상당히 들어가 있어 추가 연구가 필요하다.
- Microphone이 하나인 single-channel 모델이다.
- Clean speech 환경이다. (noisy하고 reverbrant한 환경에서는 성능 안좋음)
- 겹치는 source의 수를 알고 있어야 한다. (The unknown number of speakers)
- Real-world에서 회의 상황과 같은 continuous speech spearation 문제는 풀기 힘들다.

[1] Time-domain Speech Separation

Single-channel^*에서 각기 다른 speech source를 분리하는 single-channel speech separation에 대한 문제를 먼저 정의해보자.

Single-channel : Microphone (이하 MIC)이 하나인 조건으로, 인간으로 비유를 하자면 한 쪽 귀로만 들어^Monaural 공간 정보가 없는 조건을 말하며, MIC 개수를 언급할 때에는 channel로 표기함 (e.g., signle-channel, multi-channel etc.)

[1]-(1) Problem Statement

길이가 $T$이고, $C$개의 speech source가 섞여 있는 discrete-time waveform input mixture인 $x(t) \in \mathbb{R}^{1\times T}$ 가 주어졌다고 하자. 이 때, $C$개의 source들은 각 $s_1(t), s_2(t), …,s_C(t) \in \mathbb{R}^{1\times T}$로 표기하며, 이 source들을 time-domain에서 직접 estimation 해내는 것을 목표로 한다.

\[x(t) = \sum^C_{i=1}s_i(t)\]

전반적으로, 다음 block diagram을 따라 separation이 진행된다.

Figure. 2 Time-domain Audio Separation Network Block Diagram

★ 기본적으로 frame단위의 mixture에 대한 latent represenatation에 각 source에 해당하는 mask들을 씌워 separation한다.

[1]-(2) Input

$x(t) \in \mathbb{R}^{1\times T}$를 길이가 $L$인 $\hat{T}$개의 overlapping segment $\mathbf{x}_k \in \mathbb{R}^{1\times L}$로 나누어 준다. (단, $k=1,…,\hat{T}$)
$\hat{T}$개의 waveform segment $\mathbf{x}_k$ 들을 각각 encoder 단으로 넣어준다.

실제 구현 상에는 $X\in\mathbb{R}^{\hat{T}\times L}$이 한꺼번에 encoder로 들어가는 것이지만, 아래 설명은 각 segment (또는 frame) 별로 다뤄지고 있다. $L$은 frame 개수를 결정하는 아주 중요한 hyperparameter로, 뒤에 설명하겠지만 작을수록 성능이 좋아졌다. 물론 $L$이 작아지면 $\hat{T}$는 커진다.

[1]-(3) Convolutional Autoencoder

Mixture signal에 대한 STFT representation을 convolutional encoder/decoder로 대체하게 된 배경은 speech separation에 optimized된 audio representation을 만들어주기 위한 것

Encoder

Encoder는 waveform mixture에 대한 segment $\mathbf{x}_k \in \mathbb{R}^{1\times L}$를 길이 $N$인 latent represenation $\mathbf{w} \in \mathbb{R}^{1 \times N}$로 speech separation에 optimal하게 encoding해준다.

Encoder를 matrix multiplication 형태로 써주면 다음과 같다.

\[\mathbf{w}=\mathcal{H}(\mathbf{x}\mathbf{U})\]

$\mathbf{U}\in \mathbb{R}^{L\times N}$ : Encoder basis function 역할을 하는 길이가 $L$인 vector $N$개로 구성된 matrix (논문에는 $N\times L$로 잘못 나와있음)
$\mathcal{H}(\cdot)$ : Optional nonlinear function
- 이전 다른 모델들은 nonlinear activation function인 ReLU (Rectified Linear Unit)을 써서 encoded represenation의 non-negativity를 보장해주었다.
- Conv-TasNet에서는 여러 조건에서의 실험을 통해 linear encoder와 decoder에 non-negative constraint을 주는 것보다 sigmoid activation을 써주는 것이 더 좋은 성능을 낸다는 것을 밝혀냈다.

Decoder

Decoder를 거치면 mask가 씌워진 각 estimated source에 대한 latent representation $\mathbf{d}_i\in1\times L$를 길이 $L$인 waveform source $\hat{\mathbf{s}}_i,\ i=1,2,…,C$를 reconstruction하게 된다.

\[\hat{s}_i=\mathbf{d}_i\mathbf{V}\]

$\mathbf{d}_i\in\mathbb{R}^{1\times L}$ : Separator에서 생성한 mask로 추정된 $i$ 번째 source에 대한 latent representation
$\mathbf{V}\in \mathbb{R}^{N\times L}$ : Decoder basis function matrix

Implementation

실제 모델 구현에선, encoder와 decoder에 각각 1-D convolutional layer와 1-D transposed convolutional layer를 쓰는데, 각 segment들을 overlapping 하기 쉬워 빠르게 training할 수 있고, 모델이 더 잘 수렴한다. (PyTorch 1-D transposed convolutional layers)

Encoder/decoder representation의 특징에 대해선 다음 글에서 상세하게 다룰 예정.

[1]-(4) Separator Part

$C$개의 vector (또는 mask) $\mathbf{m}_i \in \mathbb{R}^{1 \times N}, i=1,2,…,C$를 추정해낸다.

(단, $\sum^{C}_{i=1} \mathbf{m}_i = \mathbf{1}$)

→ Mask를 추정하는 방법은 잠시 후 자세히..
Mixture representation $\mathbf{w} \in \mathbb{R}^{1 \times N}$에 각 $\mathbf{m}_i$를 element-wise multiplication을 하게 되면, 각 source의 encoded representation $\mathbf{d}_i \in \mathbb{R}^{1 \times N}$ 이 나온다. 간단히 말해, mixture에 weighting function (mask)를 씌워 source separation을 한다.

\[\mathbf{d}_i = \mathbf{w}\odot\mathbf{m}_i\]

[2] Convolutional Separation Module

[2]-(1) Properties of Separator

Mixture $\mathbf{x}$에서 각 source $s_i$를 separation하기 위한 mask $\mathbf{m}_i$를 추정하는 module이다.
Temporal Convolutional Network (TCN)에서 영감을 받아, 1-D dilated convolutional block을 여러 층 쌓아 fully-convolution 구조로 구성되어 있다.
- Sequence modeling에 쓰이는 RNN 계열 모델은 Long-term dependency를 보는 데에 유용하게 쓰이지만, recurrent connection 때문에 parallel processing에 제한이 있어 느리다.
- 따라서, RNN 계열 모델을 대체하여 Long-term dependency를 볼 수 있고, Parallel processing이 가능한 TCN을 사용한 것이다.
Standard convolution 대신에 쓰인 depth-wise convolution은 parameter 수와 compuational cost를 줄여주었다.

[2]-(2) Temporal Convolutional Network (TCN)

이 모델에서 쓰인 TCN 구조는 WaveNet에서 쓰인 dilated convolution과 residual path, skip-connection path 구조를 가져와 응용한 구조이다. 각기 다른 dilation factor를 가진 dilated convolution block들을 이용해 큰 temporal context window를 만들어 줄 수 있어, speech signal의 long-range dependency를 잡아내는 역할을 한다.

아래 Figure 3는 WaveNet에서 쓰인 dilated convolution block 구조인데, $X=4$인 한 layer들을 표현한 것이다.

Figure 3. Visualization of a Stack of Dilated Causal Convolutional Layers
(출처 : DeepMind log)

이러한 dilated convolution block들을 포함한 TCN 구조의 Conv-TasNet 전체 block diagram을 보면 다음과 같다.

Figure 4. Conv-TasNet Block Diagram
(출처 : SAPL Seminar Material by Ph.D candidate 변재욱)

각 dilated convolution block은 $X$개의 각 1-D convolutional block들로 이루어져 있고, 각 block의 dilation factor는 $1, 2, 4, …, 2^{X-1}$ 로 증가하는 형태를 띈다. 또한, 이 block는 $R$ 번 반복된다.

최종 TCN의 출력은 kernel size가 1인 $1\times 1$ convolution (a.k.a point-wise convolution)을 통과하게 되고, non-linear activation function인 sigmoid function를 지나 $C$ 개의 mask vector를 추정한다.

[2]-(3) 1-D Convolutional Block

TCN의 dilated convolution block에서 반복적으로 쓰인 1-D convolutional block을 자세히 알아보자.

각 block의 입력은 출력과 길이를 같게 해주기 위해, zero-padding 해준다.
Residual path : 각 block의 input을 다음 block으로 넘겨준다.
Skip-connection path : 각 block에서 나오는 output을 더해 최종 TCN의 출력으로 사용한다.
MobileNet에서 쓰였던 depthwise separable convolution $S\text{-}conv(\cdot)$ 테크닉을 가져와 standard convolution을 대체하여 Parameter 수를 줄여주었다.

Figure 5. 1-D Convolutional Block

Depthwise separable convolution

$S\text{-}conv(\cdot)$는 Figure 5 처럼 차례로 depthwise convolution $D\text{-}conv(\cdot)$와 pointwise convolution $1\times 1\text{-}conv(\cdot)$으로 구성되어 있다. (처음에 보이는 $1\times 1\text{-}conv(\cdot)$는 bottleneck)

$\mathbf{Y}\in\mathbb{R}^{G\times M}$: $S\text{-}conv(\cdot)$의 입력
$\mathbf{K}\in\mathbb{R}^{G\times P}$ : Size $P$의 convolutional kernel
$\mathbf{y}_j\in\mathbb{R}^{1\times M}$ : 행렬 $\mathbf{Y}$의 $j$ 번째 row
$\mathbf{k}_j\in\mathbb{R}^{1\times P}$ : 행렬 $\mathbf{K}$의 $j$ 번째 row

$D\text{-}conv(\mathbf{Y},\mathbf{K})$ 는 입력 $\mathbf{Y}$의 각 row와 상응하는 행렬 $\mathbf{K}$의 row에 대해 convolution 연산을 한다.
\[D\text{-}conv(\mathbf{Y},\mathbf{K}) = \text{concat}(\mathbf{y}_j\circledast \mathbf{k}_j),\ j=1,...,N\]
$S\text{-}conv(\mathbf{Y},\mathbf{K},\mathbf{L})$는 $D\text{-}conv(\mathbf{Y},\mathbf{K})$ 와 convolutional kernel $L$의 convolution으로, $1\times 1\text{-}conv(\cdot)$를 통해 linear하게 feature space로 변환해준다.
- $L \in \mathbb{R}^{G\times H\times 1}$ : Size 1의 convolutional kernel

\[S\text{-}conv(\mathbf{Y},\mathbf{K},\mathbf{L})=D\text{-}conv(\mathbf{Y},\mathbf{K}) \circledast \mathbf{L}\\\]

Figure 6. Depthwise Separable Convolution
(출처 : Medium log)

Kernel size $\mathbf{\hat{K}} \in \mathbb{R}^{G\times H \times P}$의 standard convolution과 비교하여, depthwise separable convolution은 $G\times P+G\times H$개의 parameter로 모델 사이즈를 대략 $P$만큼 줄였다.

PReLU & gLN

Parametric Rectified Linear Unit (PReLU)
\[\text{PReLU}(x) = \begin{cases} x, & \text{if $x \geq 0$}\\ ax, & \text{otherwise} \end{cases}\]
- $a$는 학습 가능한 parameter이다.
- Activation function의 역할로, 음의 영역에서도 0이 아닌 gradient $a$를 갖는 non-linearity를 보장해주기 위해 PReLU가 사용되었다.
Global Layer Normalization (gLN)
- Feature $\mathbf{F}\in\mathbb{R}^{N\times T}$가 channel과 time dimension에 대해서 normalization된다.
- $\gamma,\beta\in\mathbb{R}^{N\times1}$은 learnable parameter들이며, $\epsilon$은 수치적 안정성을 위한 작은 상수이다.

\[\text{gLN}(\mathbf{F}) = \frac{\mathbf{F}-\text{E}[\mathbf{F}]}{\sqrt{\text{Var}[\mathbf{F}]+\epsilon}}\odot\gamma+\beta\\ \text{E}[\mathbf{F}]=\frac1{NT}\sum_{NT}\mathbf{F}\\ \text{Var}[\mathbf{F}]=\frac1{NT}\sum_{NT}(\mathbf{F}-\text{E}[\mathbf{F}])^2\]

[2]-(4) Bottleneck Layer

Separation module의 앞 부분에는 Figure 4에서 보이는 것처럼 linear $1\times 1\text{-}conv(\cdot)$ block 하나가 bottleneck layer로써 존재한다.
- 이는 feature dimension 즉, input channel과 convolutional block들 간의 residual path의 channel 수를 뜻하는 $B$를 결정하는 역할을 한다.
Figure 5를 보면, 1-D conv block의 앞,뒤 부분에도 $1\times1\text{-}conv(\cdot)$가 존재하는데, 이 또한 bottleneck layer로써 feature dimension을 결정해준다.
- 예를 들어, 1-D conv block의 input channel이 $B$라고 하면, 앞 부분의 $1\times1\text{-}conv(\cdot)$에 의해 $H$로 확장해준다. 또한, depthwise separable convolution을 거친 후 뒷부분에 있는 $1\times1\text{-}conv(\cdot)$에 의해 $H$를 skip connection 및 output의 channel은 각각 $B$ 및 $Sc$로 변환된다.
- Conv-TasNet에서 가장 높은 성능을 보이는 hyperparameter 설정은 $B = Sc$이기 때문에 skip-connection과 residual-path를 거칠 때에는 같은 channel 개수가 적용 되겠다.

Reference

본 글에서 사용된 자료들 중, 따로 출처를 밝힌 자료를 제외한 모든 자료들은 Conv-TasNet 논문에서 가져와 사용되었습니다.

Share on

Twitter Facebook LinkedIn

deeesp