[Speech] Sound Perception 소리의 인지

Speech separation용 dataset을 튜닝하다가, sound source의 크기에 대한 특정 기준이 필요하여 소리의 크기 또는 세기에 대한 척도인 intensity와 loudness를 다시 공부하면서 정리하게 되었다. 맨날 헷갈려서 미래에 또 헷갈릴 나를 위해 정리..

소리의 intensity와 loudness를 나타내는 방법을 알아보기 전에, sound power와 sound pressure에 대해 짚고 넘어가보자.

[1] Sound Power ^음력 & Sound Pressure ^음압

Sound power와 sound pressure의 관계는 히터에 비유가 되곤 한다.

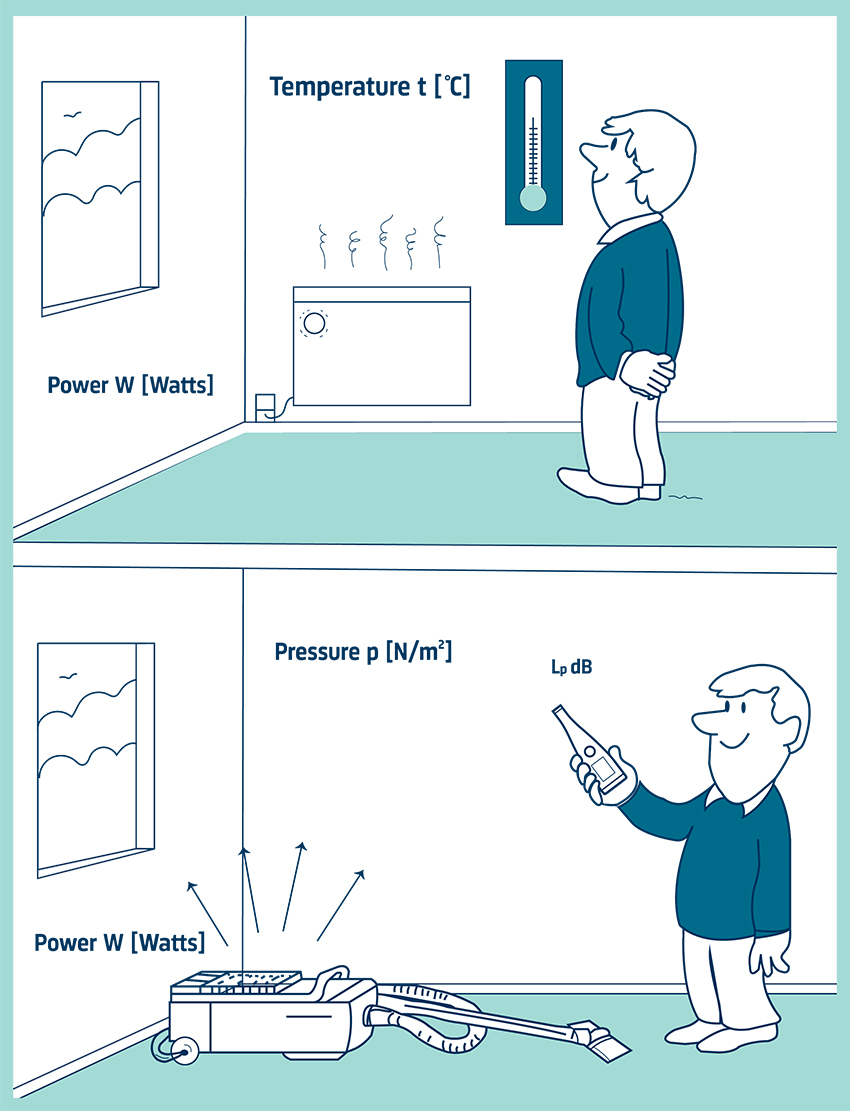
Figure 1 Sound & heater analogy
(출처 : bksv.com)

Sound Power

Sound power 는 sound source에서 공기 중으로 방출되는 단위 시간당 소리의 energy 또는 power를 말하며, 단위는 $\text{J/s}$ 또는 Watt ($\text{W}$)이다.

Sound power는 히터의 출력에 비유가 된다. 히터는 단위 시간당 특정 양의 열 (power)을 발생시켜 실내 온도를 높이는데, 이 히터의 출력은 히터가 있는 방의 특성 (크기, 표면 재질 등)과는 무관하다. 이처럼 sound power도 sound source가 발생시키는 energy는 방의 특성과 무관하다.

Sound Pressure

Sound source로부터 방출된 sound power는 공기 중으로 전달되면서 그 진동으로 압력의 변화를 만든다. Sound pressure 는 특정 환경, 특정 위치에서 이러한 순간 압력을 측정한 결과로, 단위는 $\text{N/m}^2=\text{Pascal}\ (\text{Pa}$)이다. 상대적인 값을 나타내는 sound pressure level과 혼동되지 않기 위해 sound pressure를 sound pressure amplitude level라고 나타내는 경우도 있다.

Sound pressure 는 실내 온도에 비유가 된다. 실내 온도는 히터의 출력과 다르게 히터와의 거리, 방의 크기 및 방의 내장재 등 방의 특성에 따라 달라진다. Sound pressure도 sound power와 다르게 source와의 거리 및 방의 특성에 따라 물리량이 달라진다. 방의 특성에는 방의 크기와 방의 표면 재질로 인해 흡수 및 반사하는 정도 등이 있다.

[2] Sound Intensity ^{소리의 강도} : Physical Quantity of Sound

Sound의 intensity 또는 strength 는 소리의 강도를 정량적으로 나타낼 수 있는 물리량이다. 뒤에 나올 psychoacoustic ^{심리음향적} sound level은 subjective measure인 반면 sound intensity는 obejective measure이다.

Sound의 intensity를 나타낼 수 있는 용어로는 (1) acoustic intensity, (2) audible intensity, (3) intensity level, (4) sound pressure level가 있다.

Acoustic Intensity ($I$) ^{음향 강도}

Sound의 acoustic intensity 는 단위 면적당 sound의 energy 또는 power의 평균 흐름으로 정의하며, 단위는 $\text{W/m}^2$이다. 보통 sound intensity하면 이 물리량을 말한다. 위에서 비유를 가져오면, sound intensity는 열의 흐름과 같다고 볼 수가 있다.

Figure 2 Sound intensity & pressure
(출처 : Siemens.com)

Sound intensity와 sound pressure의 관계는 다음과 같다.

\[\text{Sound Intensity}=p(t) \times v(t)\]

여기서 $v(t)$는 particle velocity^{매질의 입자속도}이며, 소리가 전달되는 동안 공기 중 입자가 진동하는 속도를 말한다. $p(t)\ [\text{N/m}^2]$는 sound pressure인데, scalar amplitude인 반면, particle velocity는 방향을 가진 vector 물리량이다. 따라서, 이 둘의 곱인 sound intensity는 ‘흐름’을 나타내는 vector 물리량이 된다. 뒤에 설명하겠지만, 이 sound intensity 측정을 위해선 particle velocity도 측정해야하는데, 이 과정이 어려우므로 대신에 sound pressure만으로 강도를 측정할 수 있는 sound pressure level (SPL)을 강도 표현에 주로 사용한다.

Audible Intensity ^{가청 강도}

Audible intensity 의 범위는 $10^{-12} \text{W/m}^2$ 부터 약 $10 \text{W/m}^2$까지이다. 이 범위의 양 끝은 각각 “사람이 들을 수 있는 최소 intensity : hearing threshold^{최소가청한계}“와 “사람이 들을 때 고통을 느끼는 threshold“를 뜻한다. 물론, 개개인마다 hearing threshold의 intensity는 다르지만, 일종의 기준을 마련하기 위해서 $I_0 = 10^{-12} \text{W/m}^2$ 로 정의한다.

Intensity Level ($IL$) ^{소리 강도}

Sound wave의 intensity level (IL)은 기준 intensity인 hearing threshold ($I_0$)에 대한 sound source ^음원의 power를 상대적인 값으로 나타낸 것이며, 단위는 decibel (dB)이다.

\[IL = 10\log_{10}\left(\frac{I}{I_0}\right)\text{dB}\]

하지만 sound intensity는 sound pressure와 particle velocity에 영향을 받는데, particle velocity는 측정이 어렵기 때문에 편의를 위하여 다음 소개할 sound pressure만을 측정하여 강도를 표현할 수 있는 sound pressure level (SPL)을 주로 사용한다.

Sound Pressure Level ($SPL$) ^{음압 레벨}

Sound pressure level (SPL) 은 IL처럼 기준 값에 대해 상대적으로 나타내지만, sound power가 아닌 sound pressure^음압을 기준으로 나타내며 dB 단위로 표현한다.

\[SPL=10\log_{10}\left(\frac{P^2}{P_0^2}\right)=20\log_{10}\left(\frac{P}{P_0}\right)\text{dB}\]

여기서 기준음압 ($P_0$)은 정상적인 청력을 가진 사람이 귀로 느낄 수 있는 최소 sound pressure을 말하며, 상온 및 대기압의 조건에서 hearing threshold intensity $I_0 = 10^{-12} \text{W/m}^2$에 상응하는 pressure amplitude이다. \(P_0=2\times10^{-5}\text{N/m}^2\)

$\text{N/m}^2$ 단위는 Pascal ($\text{Pa}$)로도 나타낼 수 있어 $P_0=20\mu\text{Pa}$로도 표기할 수 있다.

따라서, 사람이 들을 수 있는 최소 sound pressure의 SPL은 $0\text{dB}$이다. 즉, sound pressure은 공기 중 sound power로 인한 절대적인 압력의 변화를 나타내는 반면, sound pressure “level”은 사람의 귀를 기준으로 압력의 정도 정한 수치이다.

Figure 3 환경에 따른 SPL
(출처 : toa.co.in)

일반적으로, 생활소음은 40$\text{dB}$, 일상대화할 때의 평균 SPL은 50~70 $\text{dB}$이며, 음악을 들을 때의 평균 SPL은 80~90 $\text{dB}$이다. SPL은 마이크와 증폭기, average power를 계산할 수 있는 회로 등으로 구성되어 있는 sound level meter^{소음 측정기}로 측정할 수 있다.

지금까지는 소리의 크기를 절대적인 물리량으로 나타내주는 objective measure에 대해 알아보았다.

[3] Sound Loudness ^{라우드니스} : Perceptual Quantity of Sound

앞서 소리의 절대적인 크기를 나타내는 IL, SPL 등의 소리의 physical quantity들에 대해 알아보았다. 하지만 사람이 실제로 들었을 때에는 같은 SPL이어도 주파수가 다르면 소리의 크기가 다르다고 느낀다. 따라서, 사람이 실제로 청각적으로 느끼는 소리의 크기를 psychophysical^{정신물리학}적인 실험을 통해 규정한 perceptual quantity들에 대해 알아보겠다. 소리의 perceptual quantity에는 loudness level와 relative loudness가 있다.

Loudness level ^{라우드니스 레벨}

Loudness level (LL) 은 사람이 주관적으로 느끼는 소리의 감각적인 크기를 수치화한 것으로, 소리의 perceptual quantity 중 하나이다. Tone 신호^순음의 LL은 $1000\ \text{Hz}$ tone 신호의 IL 또는 SPL과 같은 크기로 들리는 어떤 특정 주파수를 가진 tone 신호의 IL 또는 SPL로 정의한다. 다시 말해, LL은 tone신호의 주파수와 IL 또는 SPL에 대한 복잡한 함수이다. LL의 단위는 $\textit{phon}$ 으로 정의하며, IL 또는 SPL이 $x\ \text{dB}$인 $1000\ \text{Hz}$ tone 신호의 LL은 $x\ \text{phon}$이다. 백문이 불여일견, LL을 잘 설명하고 있는 그래프가 아래 figure 4가 보여주고 있는 equal loudness curve^{등 라우드니스 곡선}이다.

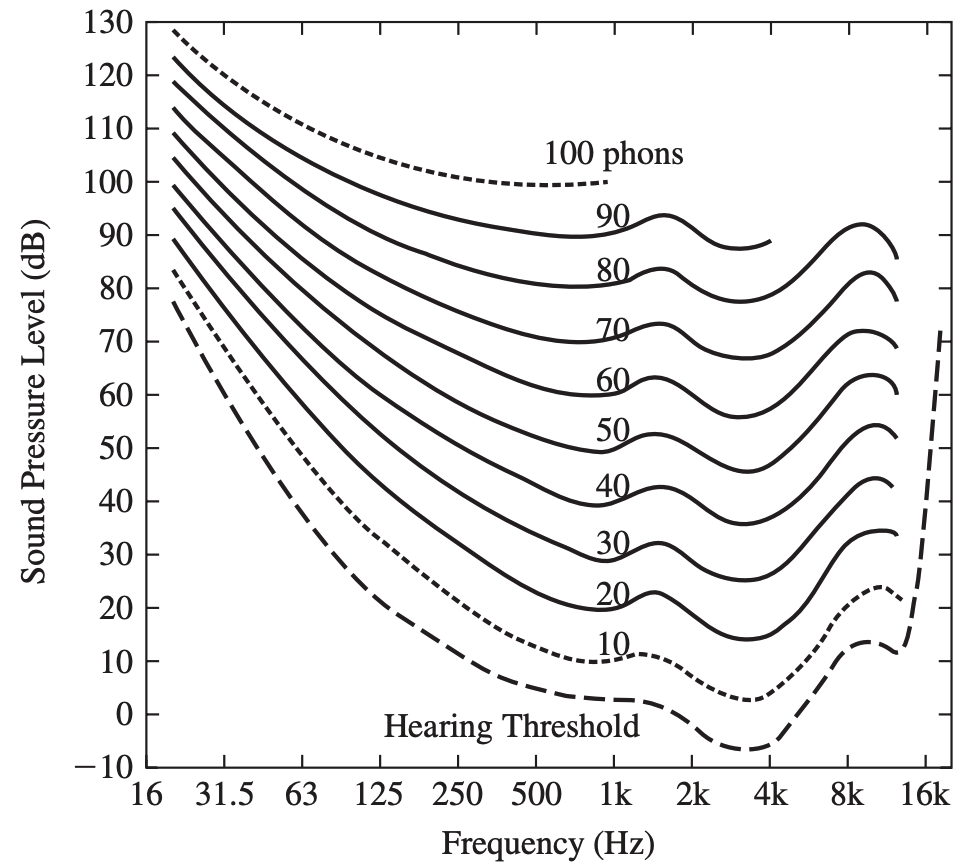
Figure 4 Equal Loudness Curve
(출처 : Theory and Applications of Digital Speech Processing)

Equal loudness curve의 가로축은 주파수, 세로축은 SPL이며, 사람이 들었을 때 같은 크기로 들리는 (즉, 같은 loudness를 가진) frequency-SPL pair들을 나타내는 곡선들로 구성되어 있다. 다시 말해, 각 곡선은 하나의 고정된 LL ($\text{phon}$ 단위)을 나타내며, 이 LL에 대해서 각 주파수에 따른 SPL을 보여주고 있다. 예를 들어, threshold of hearing의 LL은 약 $0\ \text{phon}$인데, $1000\ \text{Hz}$의 tone 신호의 SPL은 $0\ \text{dB}$인 반면 $125\ \text{Hz}$의 tone 신호의 SPL은 약 $20\ \text{dB}$이다. 즉, 두 tone 신호는 다른 SPL를 가지고 있지만 사람이 듣기에는 같은 크기로 들려 LL은 $0\ \text{phon}$로 같다.

Equal loudness curve 특성으로는 $1\text{kHz}$~$5\text{kHz}$ 대역에서 청각 감도가 높다는 것이 있다. $1\text{kHz}$와 $1.5\text{kHz}$ 사이에서 살짝 올라갔다가, $3\text{kHz}$ 부근에서 최저값을 찍으면서 떨어지는 경향을 보인다. 이 부분이 사람이 가장 민감하게 느끼는 부분이라고 볼 수 있는데, 이 부분에서 민감도가 증가하는 이유는 외이도에서의 공명효과 때문이라고 한다. 그 후 $8\text{kHz}$ 근처까지 다시 올라갔다가 $13\text{kHz}$부근에서도 살짝 떨어지는 경향을 보이다가 이후로는 주욱 올라간다. 또 다른 특성으로는 주파수가 낮을수록 곡선의 기울기가 가파르게 나타나 감도가 낮으며, 주파수가 높을수록 평탄해진다. 따라서 사람은 이러한 특성 때문에 같은 음이라도 SPL이 높은 음이 더 좋은 소리처럼 착각을 하게 된다.

매체가 디지털화가 되면서, 방송 플랫폼 간의 음량의 불균형으로 문제가 많이 나타났다. 이러한 주관적 음량을 객관화 하기 위해 ITU-R에서 표준 loudness 측정 알고리즘 권고안 ITU-R BS.1770을 발표하였고, 실제로 널리 쓰이고 있다.

Relative Loudness ^{라우드니스}

LL은 사람이 느끼기기에 크기가 같다고 느끼는 주파수별 소리들의 절대적 크기라고 알아보았다. 그러면 각기 다른 LL을 가진 소리들은 LL에 비례하게 소리가 크거나 작다고 느낄까? 정답은 아니다였다. 이런 문제를 풀기 위해 Loudness (L) 라는 개념이 탄생했다.

Reference

• L. R. Rabiner and R. W. Schafer, “Theory and Applications of Digital Speech Processing”, Pearson, 2011.
• 정보통신기술용어해설
• siemens.com
• bskv.com
• KT스카이라이프 방송운용팀