[통계] Estimation (2) - MVUE (Minimum Variance Unbiased Estimator)

한국어로 옮기면…. 최소 분산 불편 추정기… 이다. 너무 길다. MVUE로 쓰자.

앞서 Unbiased Estimator에서 보았듯이, MMSE criterion으로 만들어진 estimator는 estimation 하고자 하는 unknown parameter에 대한 함수로 만들어져 통상적으로 unrealizable하는 것을 보았다. 따라서, practical한 관점에서 MMSE estimator는 후보에서 제외한다.

[1] Alternative Approach: MVUE

• 다음과 같은 조건을 만족하는 estimator를 MVUE(Minimum Variance Unbiased Estimator) 라고 한다.

Bias가 0인 제약조건 (Constraint) 하에 Variance를 최소화 하는 estimator를 찾는다.

[2] MVUE의 존재 유무

먼저 MVUE가 존재하는 가에 대해 따져보아야 한다.

Figure 2.3의 왼쪽 그림 (a)에서는 estimator $\hat{\theta_3}$가 모든 $\theta$에 대해서 가장 작은 variance를 갖기 때문에, MVUE가 존재한다는 것을 명확히 볼 수 있다. 이러한 형태를 “Uniformly MVUE” 라고 한다.

반면에, 오른쪽 그림 (b)에서는 $\theta < \theta_0$ 에선 $\hat{\theta_2}$가 더 작은 variance를 가지고, $\theta > \theta_0$ 에선 $\hat{\theta_3}$가 더 작은 값을 가지기 때문에 모든 $\theta$에 대해서 가장 작은 variance 값을 갖는 estimator MVUE가 존재하지 않는다.

일반적으로, MVUE는 항상 존재하는 것은 아니기 때문에 존재유무를 따져보아야 한다.

[3] MVUE를 찾자

MVUE가 존재한다고 쳐도, 그걸 찾기 쉽지 않을 수 있다. Estimator를 항상 찾아내는 그럴 듯한 방법이 따로 없다는 뜻이다. 그럼 어떻게 찾는데…? 다음과 같은 방법이 있다.

1. CRLB (Cramer-Rao Lower Bound)를 결정하여 어떤 estimator가 이를 만족하는지 확인한다.
   • CRLB는 어떠한 unbiased estimator든, 특정 값보다 크거나 반드시 크거나 같다는 것을 결정해 준다.
     
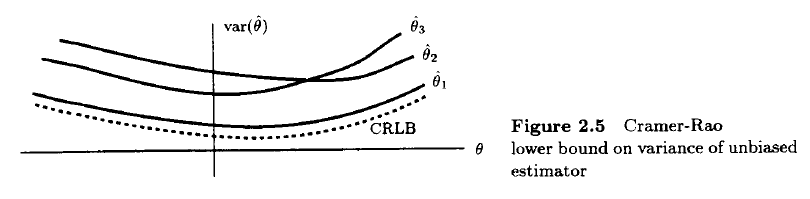
   • 어떤 estimator의 variance 값이 모든 $\theta$에 대해서 CRLB와 같다면, 무조건 MVUE이다. Estimator가 unbiased 하고 variance가 CRLB와 같다면 efficient estimator라고 한다.
   • 즉, CRLB와 같은 variance 값을 갖는 estimator가 존재하지 않을 수 있다. 그럼에도 MVUE는 존재할 수 있는데, 이 경우에는 RBLS에 의존해야 한다.
2. RBLS (Rao-Blackwell-Lehmann-Scheffe) theorem을 적용한다.
   • 먼저 observation $\textbf{x}$에 대한 함수인 sufficient statistic $T(\textbf{x})$ 를 찾는다.
   • Sufficient statistic에 대한 함수 $g(T)$로 이루어진 estimator $\hat{\theta}$를 찾는데, $\theta$에 대해 unbiased estimator이어야 한다.
3. Unbiased estimator가 linear하다고 제한하여 MVUE를 찾는다.
   • Linear하면 찾기 쉬우니깐 이러한 방법을 택할 때도 있다.

Reference

---

• [1] S. Kay. Fundamentals of Statistical Signal Processing: Estimation Theory, Prentice-Hall International Editions, Englewood Cliffs, NJ, 1993.
• [2] GIST EC7204 Detection and Estimation Lecture from Prof. 황의석