deeesp

deeesp

딥하게 신호처리 러닝 @MSPL

[DL] Activation Functions (활성화 함수)

10 minute read

DS-GA 1008 SPRING 2020 11-1

Yann LeCun 교수님의 NYU Deep Learning 강의 11-1 번역

활성화 함수

몇 가지 중요한 활성화 함수와 파이토치에서의 구현에 대해 복습할 것이다. 다양한 논문에서 어떤 특정 문제들에 대해서 여기서 다룰 활성화 함수들이 효과적이라고 동작한다고 주장했다.

ReLU - nn.ReLU()

\[\text{ReLU}(x) = (x)^{+} = \max(0,x)\]

그림. 1: ReLU 함수

RReLU - nn.RReLU()

ReLU 함수에서 변형을 준 것이다. Random ReLU(RReLU)는 다음과 같이 정의한다.

\[\text{RReLU}(x) = \begin{cases} x, & \text{if $x \geq 0$}\\ ax, & \text{otherwise} \end{cases}\]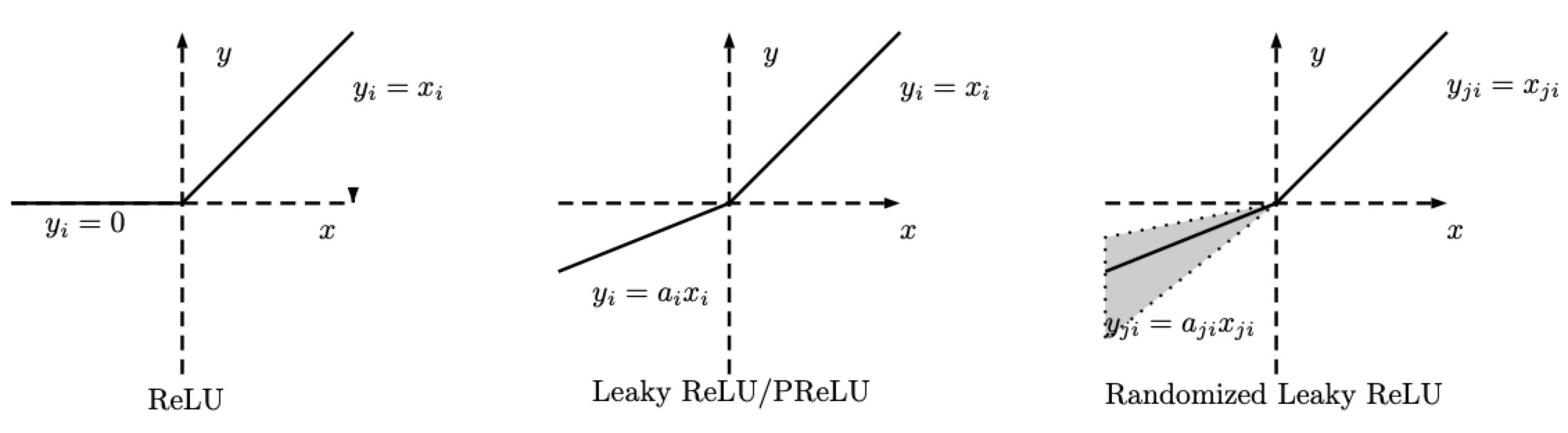

그림. 2: ReLU, Leaky ReLU/PReLU, RReLU

RReLU에서 주의해야 할 점은, $a$는 훈련 중에 주어진 범위 내에서 추출되는 확률 변수이며, 테스트할 때에는 고정 값이 된다. PReLU에서도 또한 $a$는 학습되지만, Leaky ReLU에서는 $a$는 고정 값이다.

LeakyReLU - nn.LeakyReLU()

\[\text{LeakyReLU}(x) = \begin{cases} x, & \text{if $x \geq 0$}\\ a_\text{negative slope}x, & \text{otherwise} \end{cases}\]

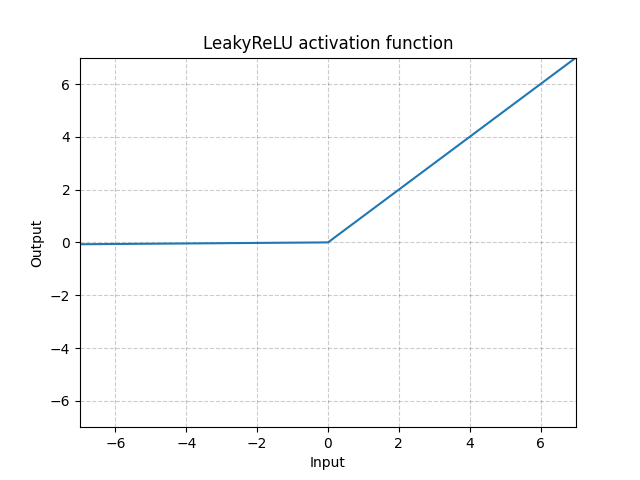
그림. 3: LeakyReLU

여기서 $a$는 고정된 매개 변수이다. 수식의 아래부분은 ReLU 뉴런이 비활성화 되는 것 즉, 어떤 입력에 대해서도 출력이 0이 되어 버리는 “Dying ReLU” 문제를 막아준다. 그러므로, 경사가 0이 된다. 음의 입력에 대한 작은 값의 기울기<sup>Negative slope</sup>를 사용함으로써, 신경망이 역전파되어 잘 학습할 수 있도록 한다.

LeakyReLU is necessary for skinny network, which is almost impossible to get gradients flowing back with vanilla ReLU.

LeakyReLU는 바닐라 ReLU를 쓴다면 경사를 역전파하는 것이 거의 불가능한 skinny network에서 필요하다. 즉, 모든 값이 0이 되어 훈련이 힘든 영역에서도 LeakyReLU를 사용하면 skinny network는 경사를 가질 수 있다.

PReLU - nn.PReLU()

\[\text{PReLU}(x) = \begin{cases} x, & \text{if $x \geq 0$}\\ ax, & \text{otherwise} \end{cases}\]

여기서 $a$는 학습 가능한 매개변수이다.


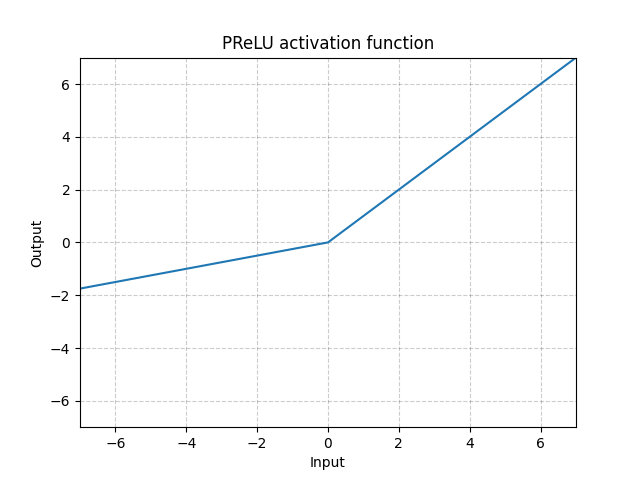
그림. 4: PReLU

위의 활성화 함수들(ReLU, LeakyReLU, PReLU)은 스케일 불변Scale-invariant하다.

Softplus - Softplus()

\[\text{Softplus}(x) = \frac{1}{\beta} * \log(1 + \exp(\beta * x))\]

그림. 5: Softplus

Softplus는 ReLU 함수를 부드럽게 근사한 것(미분 가능)으로, 출력을 항상 양수로 제한하는 데에 사용할 수 있다. $\beta$가 커질수록 ReLU와 비슷해진다.

ELU - nn.ELU()

\[\text{ELU}(x) = \max(0, x) + \min(0, \alpha * (\exp(x) - 1) \]

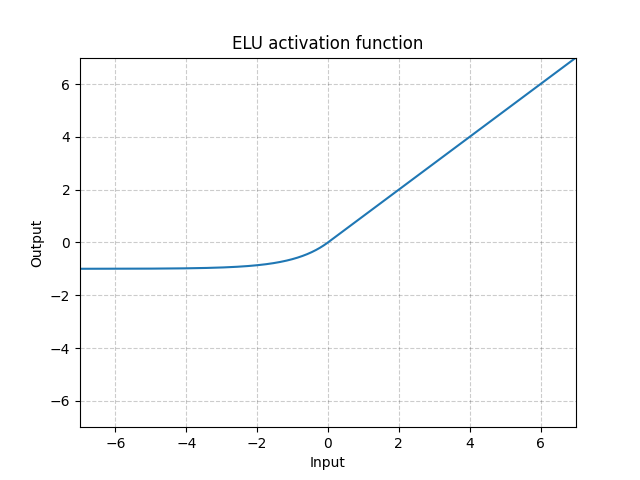
그림. 6: ELU

ReLU와는 달리, 0 이하로 내려가면 시스템의 평균 출력이 0이 될 수 있어, 모델이 더 빠르게 수렴할 것이다. CELU와 SELU는 ELU를 변형한 것으로, 단지 다른 방식으로 매개변수화한 것이다.

CELU - nn.CELU()

\[\text{CELU}(x) = \max(0, x) + \min(0, \alpha * (\exp(x/\alpha) - 1) \]

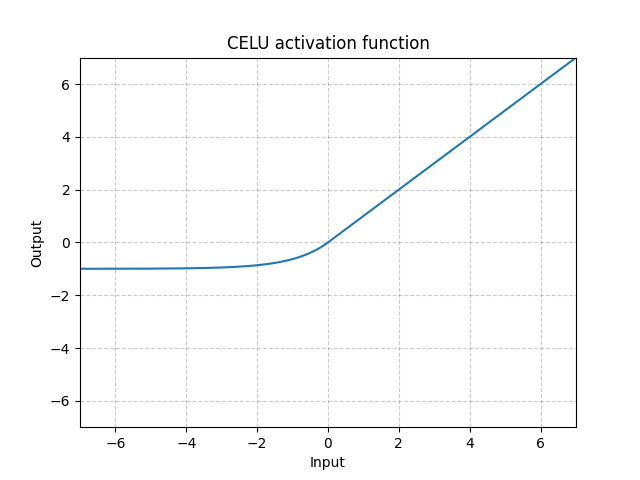
그림. 7: CELU

SELU - nn.SELU()

\[\text{SELU}(x) = \text{scale} * (\max(0, x) + \min(0, \alpha * (\exp(x) - 1)) \]

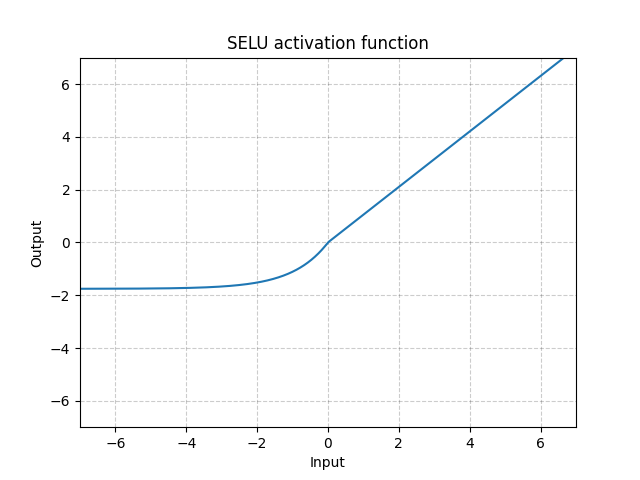
그림. 8: SELU

GELU - nn.GELU()

\[\text{GELU(x)} = x * \Phi(x) \]

여기서 $\Phi(x)$는 가우시안 분포의 누적확률분포함수(CDF)Cumulative Distribution Function이다.


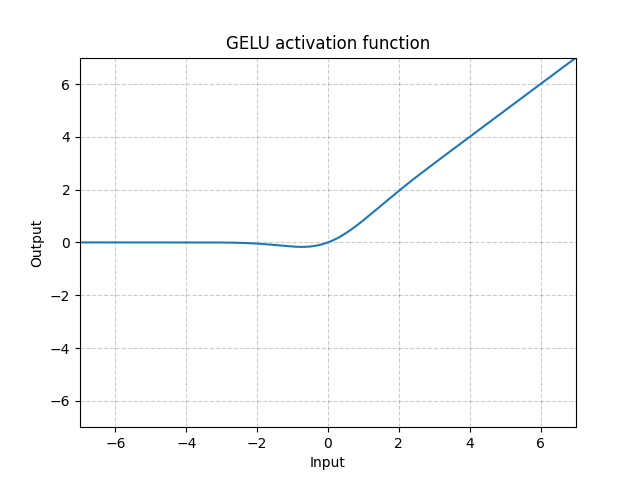
그림. 9: GELU

ReLU6 - nn.ReLU6()

\[\text{ReLU6}(x) = \min(\max(0,x),6) \]

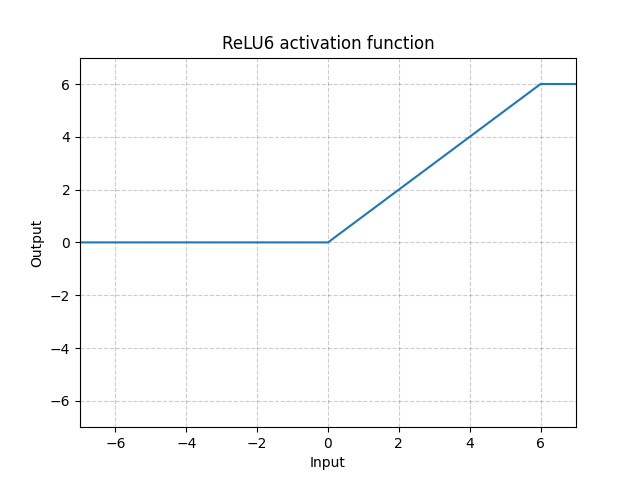
그림. 10: ReLU6

ReLU6는 6에서 포화상태가 되는Saturated ReLU이다. 그러나 6을 포화상태로 하는 데에는 특별한 이유가 없기 때문에, 아래 Sigmoid 함수를 사용하는 것이 더 좋을 수 있다.

Sigmoid - nn.Sigmoid()

\[\text{Sigmoid}(x) = \sigma(x) = \frac{1}{1 + \exp(-x)} \]

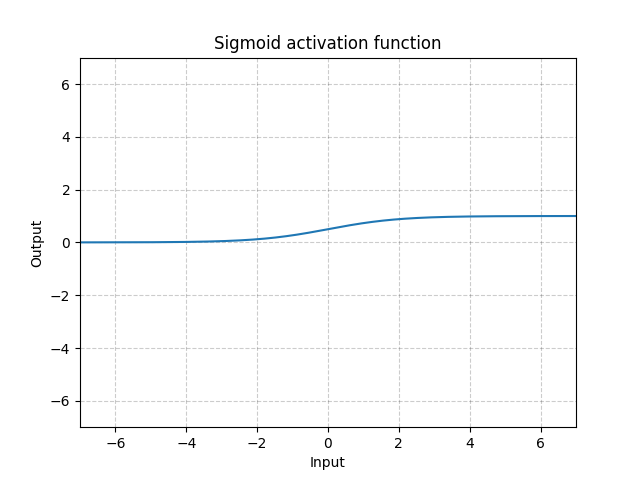
그림. 11: Sigmoid

여러 계층에 Sigmoid를 쌓으면, 학습하는데 비효율적일 수 있고 초기화에 주의해야 한다. 이는 입력이 매우 크거나 작으면 Sigmoid의 기울기가 0에 가까워지기 때문이다. 이 경우, 매개변수를 업데이트 하기 위해 역전파 되는 경사가 없게 되는데, 이를 경사포화문제Saturating gradient problem라고 한다. 그러므로, 심층 신경망에서는 ReLU와 같은 단일 Kink 함수A single kink function(미분 불가능한 점이 하나 존재하는 함수)가 선호된다.

Tanh - nn.Tanh()

\[\text{Tanh}(x) = \tanh(x) = \frac{\exp(x) - \exp(-x)}{\exp(x) + \exp(-x)}\]

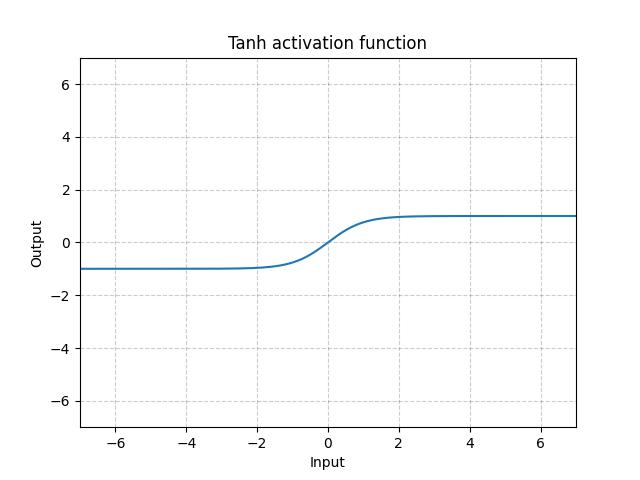
그림. 12: Tanh

Tanh는 -1에서 1까지의 범위에 집중되어 있다는 점을 제외하면 기본적으로 Sigmoid와 동일하다. 함수 출력의 평균은 거의 0에 가까우므로, 모델이 빨리 수렴하게 된다. 일반적으로 각 입력 변수의 평균이 0에 가까울수록 수렴속도가 빠르다는 것에 유의해야 한다. 배치 정규화Batch Normalization가 그 예시이다.

Softsign - nn.Softsign()

\[\text{SoftSign}(x) = \frac{x}{1 + |x|}\]

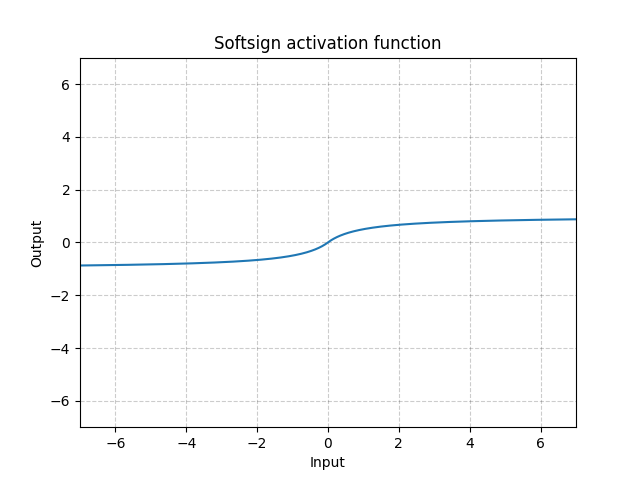
그림. 13: Softsign

Sigmoid 함수와 비슷하지만, 점근선Asymptote에 천천히 도달하여 경사소실문제Gradient Vanishing Problem를 어느정도 완화해준다.

Hardtanh - nn.Hardtanh()

\[\text{HardTanh}(x) = \begin{cases} 1, & \text{if $x > 1$}\\ -1, & \text{if $x < -1$}\\ x, & \text{otherwise} \end{cases}\]

선형 영역[-1, 1]의 범위는 min_val 과 max_val를 이용하여 조정할 수 있다.


그림. 14: Hardtanh

Hardtanh는 놀랍게도 가중치가 작은 값 범위 내에 있을 때 놀랍게도 잘 작동한다.

Threshold - nn.Threshold()

\[y = \begin{cases} x, & \text{if $x > \text{threshold}$}\\ v, & \text{otherwise} \end{cases}\]

Threshold는 경사를 역전파할 수 없기 때문에 거의 사용되지 않는다. 60~70년대에 이진뉴런을 사용할 때, 역전파를 사용하지 못했던 이유이기도 하다.

Tanhshrink - nn.Tanhshrink()

\[\text{Tanhshrink}(x) = x - \tanh(x) \]

그림. 15: Tanhshrink

Thanshrink는 잠재변수 값을 계산하기 위한 희소 코딩Sparse coding 외에는 거의 사용되지 않는다.

Softshrink - nn.Softshrink()

\[\text{SoftShrinkage}(x) = \begin{cases} x - \lambda, & \text{if $x > \lambda$}\\ x + \lambda, & \text{if $x < -\lambda$}\\ 0, & \text{otherwise} \end{cases}\]

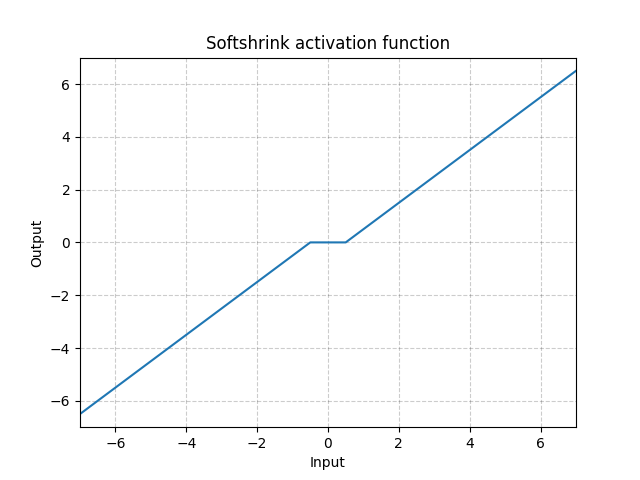
그림. 16: Softshrink

Softshrink는 기본적으로 변수를 0을 향해 상수로 수축시키고, 변수가 0에 가까워지면 출력은 0이 된다. $\ell_1$ 기준에 대한 경사라고 생각하면 된다. Softshrink를 Iterative Shrinkage-Thresholding Algorithm (ISTA)의 특정 단계에서 쓰이기도 하다. 그러나 일반적인 신경망에서 활성화로는 잘 사용되지 않는다.

Hardshrink - nn.Hardshrink()

\[\text{HardShrinkage}(x) = \begin{cases} x, & \text{if $x > \lambda$}\\ x, & \text{if $x < -\lambda$}\\ 0, & \text{otherwise} \end{cases}\]

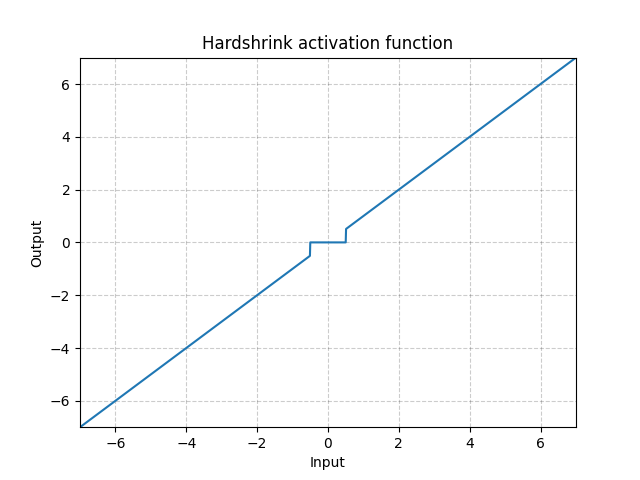
그림. 17: Hardshrink

Hardshrink 또한 희소 코딩Sparse coding을 제외하고는 거의 사용되지 않는다.

LogSigmoid - nn.LogSigmoid()

\[\text{LogSigmoid}(x) = \log\left(\frac{1}{1 + \exp(-x)}\right) \]

그림. 18: LogSigmoid

LogSigmoid는 주로 활성화함수 보다는 손실함수에 사용된다.

Softmin - nn.Softmin()

\[\text{Softmin}(x_i) = \frac{\exp(-x_i)}{\sum_j \exp(-x_j)} \]

Softmin은 숫자를 확률분포로 변환한다.

Soft(arg)max - nn.Softmax()

\[\text{Softmax}(x_i) = \frac{\exp(x_i)}{\sum_j \exp(x_j)} \]

LogSoft(arg)max - nn.LogSoftmax()

\[\text{LogSoftmax}(x_i) = \log\left(\frac{\exp(x_i)}{\sum_j \exp(x_j)}\right) \]

LogSoft(arg)max 또한 활성화 함수에는 잘 안쓰이고 주로 손실함수에 사용된다.

Q&A 활성화 함수

nn.PReLU() 관련된 질문들

  • 왜 모든 채널에 대해 같은 $a$ 값이 필요한가요?

    각 채널들은 다른 $a$ 값을 가질 수 있다. $a$를 모든 유닛의 매개변수로 사용할 수 있다. 또한, 특징지도Feature map로 공유될 수 있다.

  • $a$를 학습하나요? $a$를 학습함으로써 얻는 이점이 있나요?

    $a$를 학습할 수도 있고 고정시킬 수도 있다. 고정시키는 이유는 음의 영역에서도 0이 아닌 경사를 갖는 비선형성을 보장하기 때문이다. $a$를 학습가능하도록 만듦으로써 시스템을 비선형성에서 선형 매핑 및 완전정류Full rectification로 변환할 수 있다. 이는 윤곽선Edge의 극성에 무관한 윤곽선 검출을 구현과 같은 응용에 사용될 수 있다.

  • 얼마나 비선형성을 복잡하게 만들 수 있나요?

    이론적으로, 스프링 매개변수<sup>Spring parameter</sup>와 체비셰프 다항식 등과 같이 전체 비선형 함수를 아주 복잡한 방법으로 매개변수화 시킬 수 있다. 매개변수화 시키는 것은 일종의 학습 방법이다.

  • 시스템에서 유닛을 많이 가지고 있는 것보다 매개변수화 하는 것의 이점이 무엇인가요?

    무엇을 하고 싶은지에 달려있다. 예를 들어, 저차원 공간에서 회귀 분석을 수행할 때에는, 매개변수화 하는 것이 도움이 될 수 있다. 그러나 이미지 인식과 같이 고차원 공간을 다루는 경우, “a” 비선형성이 필요할 것이고 단조 비선형성Monotonic nonlinearity이 더 효과적일 것이다. 간단히 말해, 어떠한 함수도 매개변수화할 수 있지만, 큰 이점을 가져오지는 않을 수 있다.

  • 단일 Kink vs 이중 Kink

이중 kink가 기본 스케일이다. 이말인 즉슨, 입력 층에 2가 곱해지면(또는 신호의 진폭에 2를 곱하면), 출력은 완전히 달라질 것이다. 이 신호는 비선형에 더욱 가까워질 것이고, 완전히 다른 특성을 갖는 출력을 얻을 것이다. 반면에 단일 kink 함수라면, 입력에 2를 곱해도 출력 또한 2를 곱한 값이 될 것이다.

  • 꺾인 비선형 활성화와 부드러운 비선형 활성화의 차이점, 언제 어떤 것이 왜 선호되나요?

이는 Scale equivariance와 관련된 문제이다. kink가 hard하면, 입력에 2를 곱했을 때 출력에도 2가 곱해진다. 부드러운 활성화의 경우로 예를 들자면, 입력에 100을 곱한다면 출력은 hard kink처럼 보이게 된다. 이는 부드러운 부분이 100만큼 줄어들기 떄문이다. 반대로 입력을 100으로 나누면, kink는 아주 매끄러운 볼록함수Convex function가 된다. 따라서 입력의 스케일을 변경하여 활성화 유닛의 특성을 꿔야 한다.

하지만 이 방법은 종종 문제가 될 때가 있다. 예를 들어, 다층 신경망을 학습시킬 때 연달아 있는 두 개의 층의 경우가 그렇다. 한 층의 가중치들이 다른 층의 가중치들에 얼마나 크게 상관이 있는지를 제어할 수 없다. 스케일에 영향이 있는 비선형은 특성을 완전히 바꿔 버리기 때문에, 신경망의 첫 번째 층에서 어떤 크기의 가중치 행렬을 사용할 지 정할 수 없다.

이 문제를 해결할 수 있는 방법 중 하나는 배치 정규화Batch normalization와 같이 각 층의 가중치를에 hard scale을 설정해서 정규화 할 수 있다. 따라서 한 유닛으로 들어가는 분산이 항상 상수가 된다. 스케일을 고정하게 되면, 시스템은 이중 kink 함수 시스템에서 비선형성의 어떤 부분을 사용할지 선택할 수 있는 방법이 없다. ‘고정된’ 부분이 너무 선형에 가까워지면 문제가 된다. 예를 들어, Sigmoid는 0 부근에서 거의 선형이 되어서 (0에 가까운) 배치 정규화된 출력은 ‘비선형성’을 활성화 시킬 수 없다. 심층 신경망이 왜 단일 kink 함수에서 잘 작동하는지에 대한 이유는 명확하지는 않다. 아마도 scale equivariance 특성 때문인 것 같다.

https://s3-us-west-2.amazonaws.com/secure.notion-static.com/5a1d4de9-b572-4835-ab68-0d75851c6dcf/Untitled.png

출처: http://parker.ad.siu.edu/Olive/ch9.pdf

Soft(arg)max 함수에서의 온도계수Temperature coefficient

  • 언제 온도계수를 사용하고, 왜 사용하나요?

어느 정도까지는, 온도는 입력 가중치에 redundant하다. 가중합이 Softmax로 들어가면, $\beta$ 매개변수는 가중치의 크기와 redundant하다.

온도는 출력분포의 hard한 정도를 제어한다. $\beta$가 아주 클 때는 출력이 1이나 0에 아주 가깝게 된다. $\beta$가 아주 작으면 soft해진다. $\beta$가 0에 가깝게 한정되면 평균에 가까워진다. $\beta$가 무한대로 발산하게 되면, argmax와 같은 특성을 가져 더이상 soft한 버전이 아니게 된다. 그러므로 softmax에 넣어주기 전에 정규화Normalization를 거치면 매개변수 조정을 통해 hardness를 조절할 수 있다.

보통 작은 $\beta$에서 시작하면, 경사하강법이 적절하게 동작하도록 할 수 있고, 어텐션 메커니즘Attention mechanism과 같은 harder decision을 원한다면 $\beta$를 증가시키면 된다. 따라서, 결정을 sharpen 하게 할 수 있다. 이러한 방법을 담금질Annealing이라고 한다. Self-attention mechanism과 같은 experts의 mixture에 유용하게 사용할 수 있다.

returning a probability distribution

def softmax_with_temperature(z, beta) : 
    z = np.array(z)
    z = z * beta
    max_z = np.max(z) 
    exp_z = np.exp(z-max_z) 
    sum_exp_z = np.sum(exp_z)
    y = exp_z / sum_exp_z
    return y

출처:

https://3months.tistory.com/491

[Deep Play]

그렇다면, 왜 상수 ‘e’를 사용하는가?

  1. 아래와같이 미분이 아주 깔끔해서 입니다.

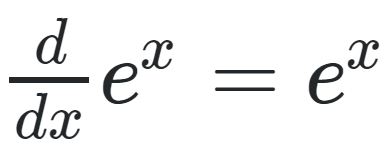
    https://blog.kakaocdn.net/dn/Mhboo/btqy7Kjz1L6/FTTWidzaqT5WwVQ74Vz450/img.png

  2. ‘soft’max의 관점에서, 입력값에 대한 결과값을 보면 ‘hard’하게 잘려있기 보다는, ‘soft’하게 나눠지는 것을 볼 수 있습니다. 그래서 max값만 출력되는, one-hot vector의 형태로 출력되는 argmax와 달리, softmax는 max에 근접한 값들도 출력이되며, 이를 이용해 손실을 계산하는것이 유익합니다. (참고로 hardmax는 미분이 불가능하며, soft는 어디에서든지 미분이 가능합니다.)
    • argmax ([1, 3, 0, 2]) = [0, 1, 0, 0]
    • soft arg max([1, 3, 0, 2]) ≈ [0.087 0.644 0.032 0.24]
  3. soft’max’의 관점에서, max이려면 차이가 얼마 안나도 가장 큰 값이 확실하게 구별될 정도로 크게 나타나야하기에, e를 사용하면, 지수승으로 표현이 가능해서 값의 비교가 명확해짐. 다른말로 하면, 엔트로피를 최대화하는 손실함수가 softmax입니다.

Leave a comment

You may also enjoy