[DL] 신경망 매개변수의 변환과 합성곱의 개념
DS-GA 1008 SPRING 2020 03-1
Yann LeCun 교수님의 NYU Deep Learning 강의 03-1 번역
신경망 시각화
이 절에서는 아래 그림 1과 같이 신경망 내부가 어떻게 동작하는지 구조를 알아보겠다.
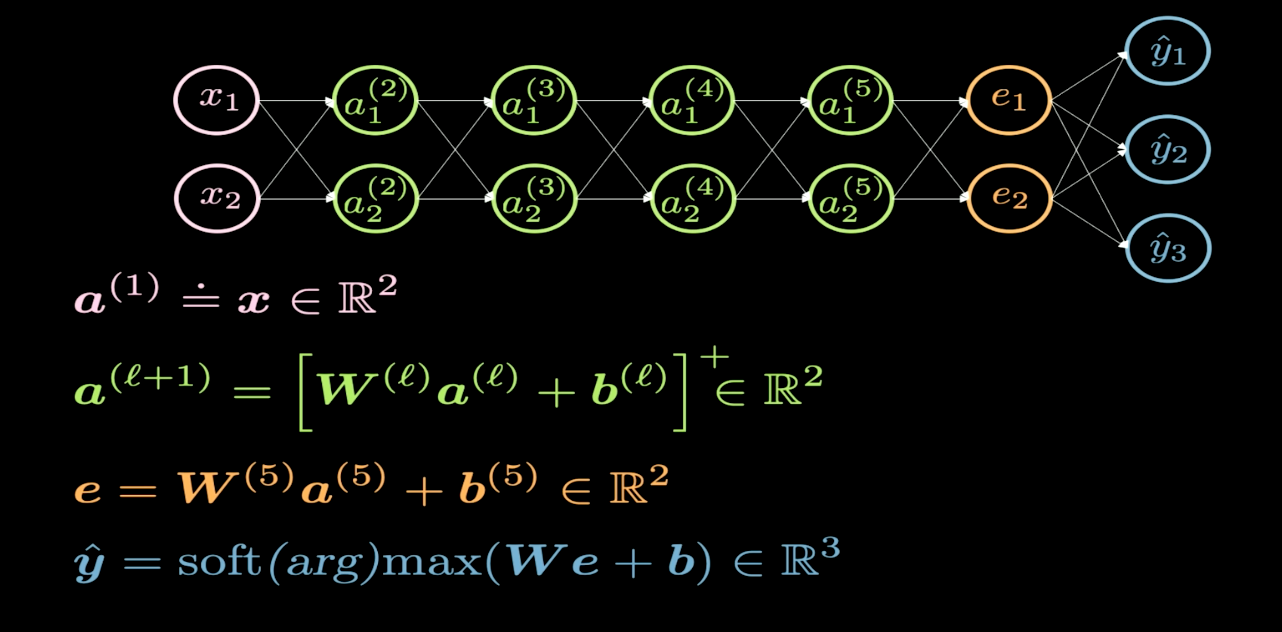
그림. 1 신경망 구조
일반적으로 신경망의 구조를 그릴 때, 입력은 아래나 왼쪽에 나타나고 출력은 위나 오른쪽에 나타난다. 그림 1을 보면, 분홍색 뉴런은 입력을 나타내고 파란색 뉴런은 출력을 나타내며, 4개의 초록색 은닉층Hidden Layers을 가지고 있다. 즉, 총 6개 층으로, 4개의 은닉층과 1개의 입력 층, 1개의 출력 층을 가지고 있다. 이 예시에서 보여주는 신경망은 각 은닉층마다 2개의 뉴런을 가지고 있으므로, 각 층별 가중치 행렬 ($W$)의 차원은 2X2가 된다. 이는 입력 평면을 시각화가 가능한 다른 평면으로 변환하고자 하기 때문이다.

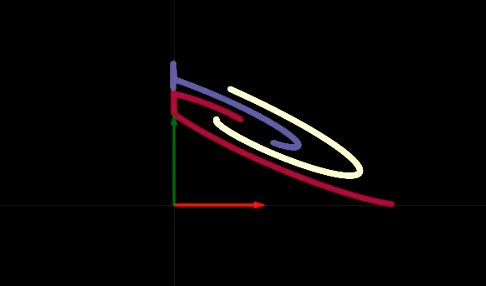
그림. 2 접힘 평면Folding space
각 층의 변환은 그림 2에서 보여지는 것처럼 특정 지역에서 평면을 접는 것과 같다. 2차원 계층에서 모든 변환이 이루어지기 때문에, 매우 갑작스럽게 접히게 된다. 각 은닉층에 2개의 뉴런만 있다면 최적화가 더 오래 걸리고, 은닉층에 많은 뉴런이 있을수록 최적화가 더 쉬워진다는 것을 실험을 통해서 발견하였다. 여기서 “왜 더 적은 뉴런으로 신경망을 학습시키는 것이 더 어려울까?”라는 의문점을 남기게 될 것이고, 우리는 이러한 질문에 스스로 생각해 보아야 한다. $\texttt{ReLU}$를 시각화 해본 뒤에 다시 돌아와 생각해 보자.
 |
|  |
|(a)|(b)|
|
|(a)|(b)|
신경망의 은닉층을 하나씩 살펴보면, 각 계층마다 아핀 변환Affine Transformation을 일부 수행한 다음, 비선형 ReLU 연산을 하여 음수 값을 모두 제거하는 것을 볼 수 있다. ReLU 연산은 비선형 변환하는 데에 쓰이며, 그림 3(a)와 (b)는 이 ReLU 연산을 시각화한 것이다. ReLU 연산 후 아핀 변환을 수행하는 과정을 여러번 거치면, 그림 4에서 볼 수 있듯이 데이터를 선형적으로 분리할 수 있다.

그림. 4 출력 시각화
왜 2개 뉴런으로만 이루어진 은닉층이 학습하기 어려운 지에 대해 감이 올 것이다. 6-계층 신경망에는 각 은닉층마다 하나의 편향Bias이 있다. 이러한 편향 중 하나가 점을 우상단 사분면 밖으로 이동시키게 되고 ReLU 연산을 취하면, 그 점은 0으로 제거되버려서 그 이후 각 층에서 데이터를 어떻게 변환하든지 값은 0으로 유지된다. 우리는 은닉층에 뉴런을 추가하는 등 네트워크를 “더 무겁게” 만들어 신경망을 보다 더 쉽게 학습시킬 수 있다. 또는 은닉층을 더 추가하거나 앞의 두 방법을 조합하는 방법도 있다. 이러한 과정을 통해 우리는 주어진 문제에 가장 적합한 신경망 아키텍처를 결정하는 방법을 계속 탐구할 것이다.
매개변수 변환 (Parameter Transformations)
일반적으로 매개변수를 변환한다는 것은 매개변수 벡터 $w$를 어떤 함수의 출력으로 본다는 것을 의미한다. 이 변환을 통해 원래 매개변수 공간을 다른 공간에 맵핑할 수 있다. 그림 5를 보면, $w$는 실제로 매개변수 $u$를 가진 $H$의 출력이다. $G(x,w)$는 신경망이며 $C(y,\bar y)$는 비용 함수Cost Function이다. 역전파Backpropagation 공식도 다음과 같이 조정된다.
\[u \leftarrow u - \eta\frac{\partial H}{\partial u}^\top\frac{\partial C}{\partial w}^\top\] \[w \leftarrow w - \eta\frac{\partial H}{\partial u}\frac{\partial H}{\partial u}^\top\frac{\partial C}{\partial w}^\top\]이 공식들은 행렬 형태로 적용된다. Terms의 차원은 일정해야 한다는 것을 꼭 명심해야 한다. $u$,$w$,$\frac{\partial H}{\partial u}^\top$,$\frac{\partial C}{\partial w}^\top$의 차원은 각각 $[N_u \times 1]$,$[N_w \times 1]$,$[N_u \times N_w]$,$[N_w \times 1]$이다. 따라서 역전파 공식의 차원은 일정하다.
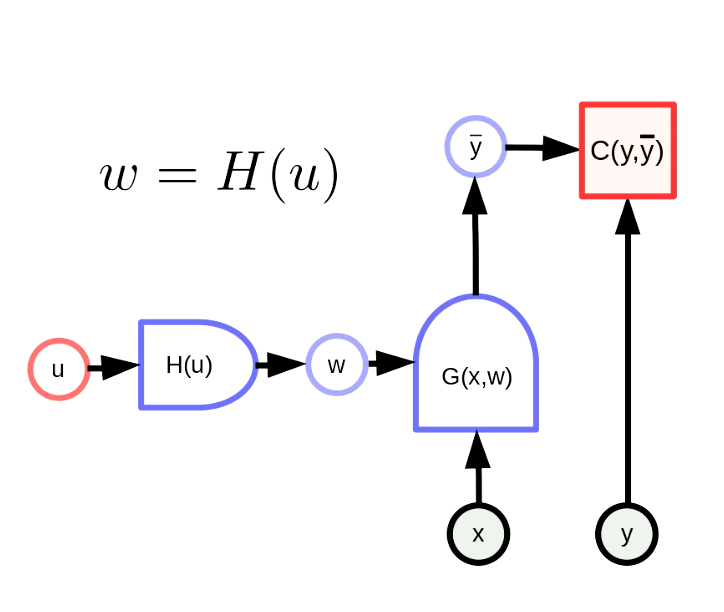
그림. 5 일반적인 매개변수 변환 형태
간단한 매개변수 변환법: 가중치 공유 (Weight Sharing)
가중치 공유 변환법은 $H(u)$가 $u$의 한 구성 요소를 여러 개의 $w$ 구성 요소로 복제하는 것을 의미한다. $H(u)$는 $u_1$를 $w_1$, $w_2$에 복사하는 Y branch와 같다. 이는 다음과 같이 표현 될 수 있다.
\[w_1 = w_2 = u_1, w_3 = w_4 = u_2\]공유 매개 변수를 동일하게 해주면, 공유 매개 변수에 대한 기울기는 역전파되면서 합산된다. 예를 들어, $u_1$에 대한 비용 함수 $C(y, \bar y)$의 기울기는 $w_1$에 대한 비용 함수 $C(y, \bar y)$의 기울기와 $w_2$에 대한 비용 함수 $C (y, \bar y)$의 기울기의 합이다.
하이퍼넷 (Hypernetwork)
하이퍼넷은 한 네트워크의 가중치가 다른 네트워크의 출력으로 구성된 네트워크를 말한다. 그림 6은 하이퍼넷의 계산 그래프를 보여준다. 함수 $H$는 매개변수 벡터 $u$와 입력 $x$로 구성된 신경망이다. 결과적으로, $G(x,w)$의 가중치는 $H(x,u)$의 출력에 의해 동적으로 구성하게 된다. 이 아이디어는 오래전에 나왔지만 여전히 강력하다.
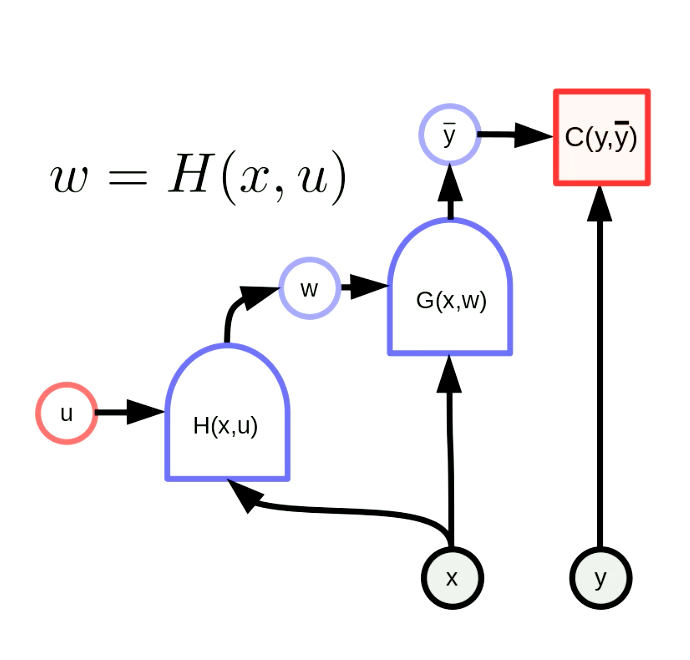
그림. 6 "하이퍼넷"
순차 데이터에서의 모티프 검출
우리는 모티프 검출Motif detection에 가중치 공유 변환을 응용할 수 있다. 모티프 검출이란 음성이나 글에 있는 “키워드”처럼 순차 데이터에 있는 모티프를 찾는 것을 말한다. 그림 7과 같이, 모티프 검출을 하기 위한 방법 중의 하나로 데이터에 슬라이딩 윈도우를 사용하는 것을 들 수 있다. 여기서, 특정 모티프(예를 들어, 음성 신호에서 특정 소리)를 검출하기 위해 가중치 공유 함수를 이동하고 출력(i.e. 점수Score)을 Maximum 함수로 넣어준다.
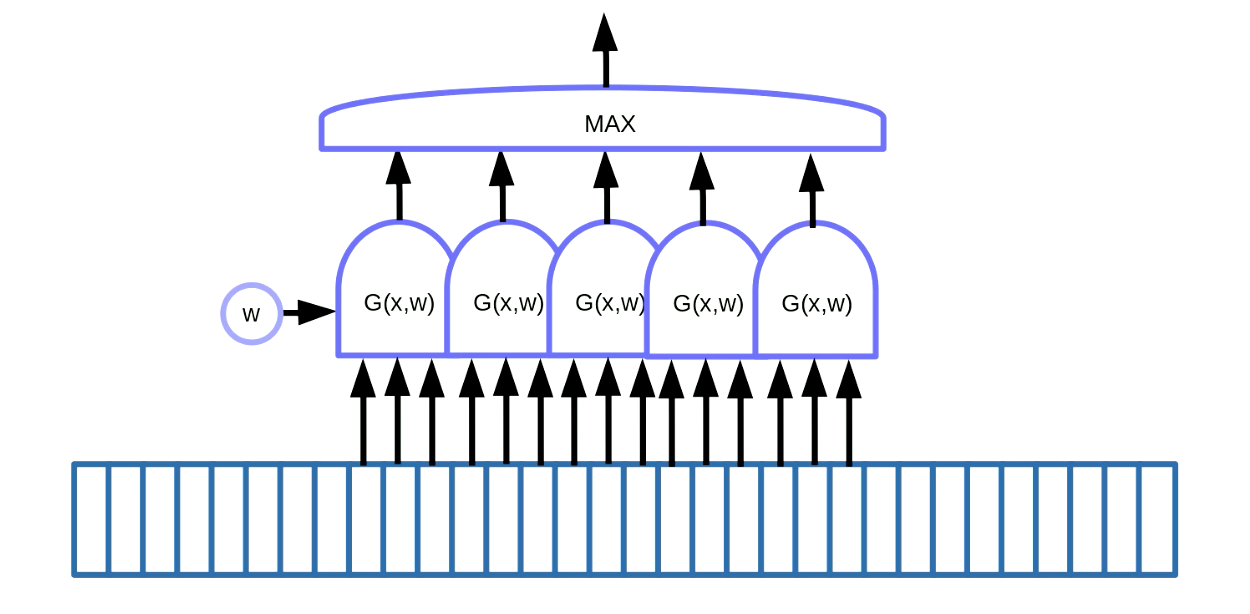
Fig. 7 순차 데이터에서 모티프 검출
이 예제에는 5개의 함수가 있다. 결과적으로 보면, 기울기 5개를 더하고 오류Error를 역전파하여 $w$ 매개변수를 업데이트 한다. PyTorch에서 구현할 때에는, 이 기울기들이 안쪽에서 축적되는 것을 막아야 하는데, 기울기를 초기화하기 위해 zero_grad ()를 사용해야 한다.
이미지에서의 모티프 검출
모티프 검출은 이미지에서도 유용하게 쓰인다. 일반적으로 이미지 위에 “템플릿”을 움직여가며 형상의 위치나 왜곡과 무관하게 검출한다. 간단히 예를 들자면, 그림 8과 같이 “C”와 “D”를 구별하는 것이다. “C”에는 두 개의 끝점End point이 있고 “D”에 두 개의 모서리Corner가 있다는 것이 “C”와 “D”의 차이점이다. 따라서 “끝점 템플릿”과 “모서리 템플릿”을 설계한다. 형상이 이 “템플릿”과 유사하면 출력이 임계 값Threshold을 가지고, 이들을 합산하여 출력의 글자를 구별 할 수 있다. 그림 8에서 네트워크는 두 개의 끝점과 모서리를 감지하여 “C”를 활성화한다.
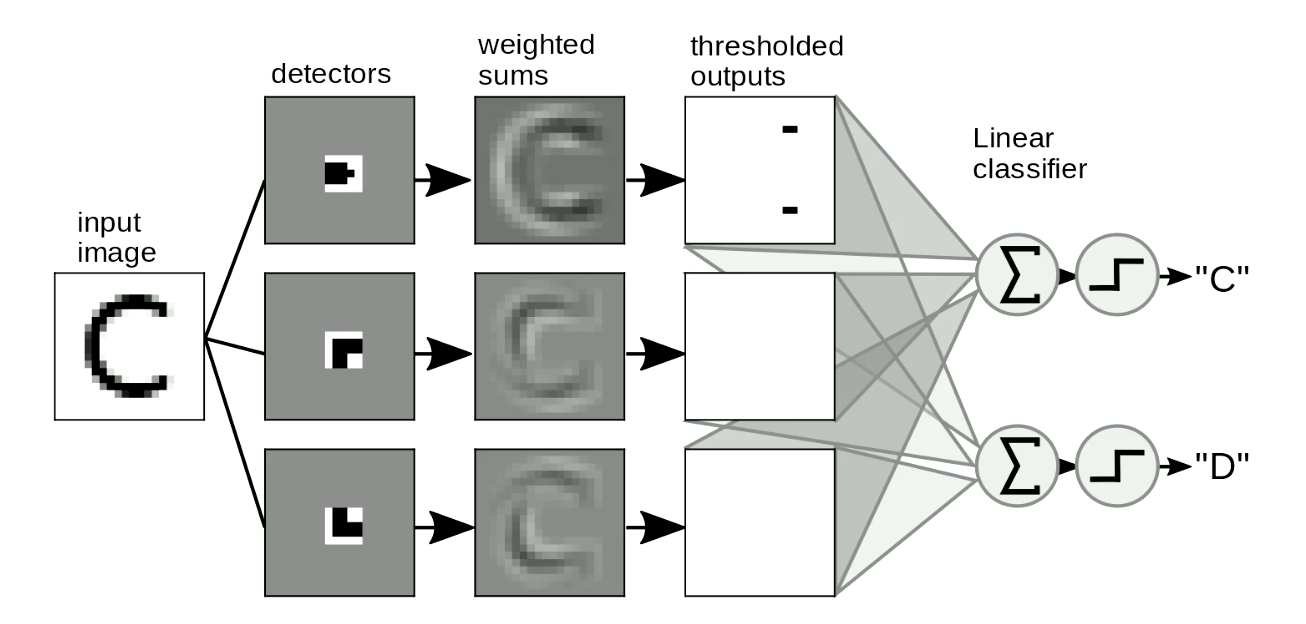
Fig. 8 이미지에서의 모티프 검출
템플릿 일치Template matching는 입력의 위치가 바뀌었을 때에도 출력(i.e. 문자 검출)은 바뀌지 않는 이동 불변한Shift-invariant 특성이 있는데, 이 또한 중요하다. 가중치 공유 변환으로 이를 해결할 수 있다. 그림 9에서, “D”의 위치가 바뀌어도 여전히 모서리 모티프를 검출한 것을 볼 수 있다. 이러한 모티프들을 종합하면 “D” 검출이 활성화 된다.
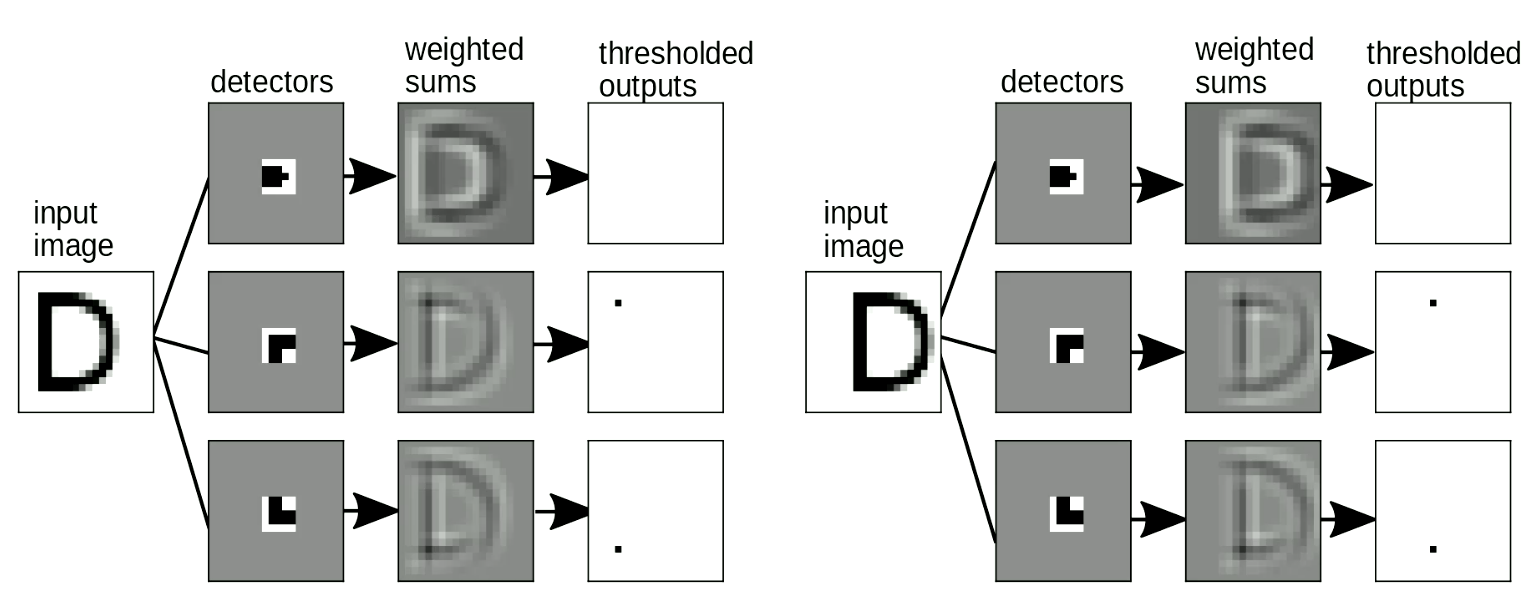
그림. 9 이동 불변성
이처럼 국부 검출기Local detector를 사용하여 합산하는 고지식한 방법은 수 년간 숫자를 인식하는 데에 많이 사용되어 왔다. 하지만 이러한 방법을 통해 우리는 “어떻게 이 템플릿을 자동적으로 설계할 수 있을까?”, “신경망을 템플릿을 학습하는 용도로 사용할 수 있을까?” 하는 생각하게 되었다. 다음으로, 이미지를 템플릿과 일치시키기 위해 사용하는 연산인 합성곱Convolutions의 개념을 소개할 것이다.
이산 합성곱 (Discrete convolution)
합성곱(Convolution)
입력 $x$와 $w$의 1차원 합성곱에 대한 정확한 수학적 정의는 다음과 같다.
\[y_i = \sum_j w_j x_{i-j}\]즉, $i$번째 출력은 수정된 $w$와 같은 사이즈의 $x$ 윈도우 간에 내적Dot product를 계산한 것이다. 전체 출력을 계산하기 위해서는, $x$를 처음부터 시작하여 끝까지 윈도우를 이동시켜가며 이 과정을 반복하는 것이다.
교차 상관관계 (Cross-correlation)
실제로는 PyTorch에서의 합성곱은 반전되지 않은 $w$로 구현되어 조금 다른 관례Convention를 따랐다.
\(y_i = \sum_j w_j x_{i+j}\) 수학자들은 이 공식을 “교차 상관관계”라고 부른다. 합성곱과의 차이점은 단지 “관례”의 차이만 있을 뿐이다. 실제로 메모리에 저장된 가중치를 앞으로 읽는지 뒤로 읽는지에 따라 교차상관과 합성곱을 서로 바꿔 쓸 수 있다.
예를 들어, 합성곱과 교차상관의 수학적 성질을 사용하고자 할 때 이러한 차이점을 인식하는 것이 중요하다.
고차원 합성곱
이미지와 같이 2차원 입력의 경우에는 2차원 버전의 합성곱을 사용한다.
\[y_{ij} = \sum_{kl} w_{kl} x_{i+k, j+l}\]위 정의는 2차원을 넘어 3차원 또는 4차원으로 쉽게 확장할 수 있다. 여기서 $w$는 합성곱 커널Convolution Kernel이다.
DCNN에서 합성곱 연산과 함께 쓰는 Regular twists
| 스트라이드 | 1 | 2 |
|---|---|---|
| 출력 크기: | $\frac{100 - (5-1)}{1}=96$ | $\frac{100 - (5-1)}{2}=48$ |
-
스트라이드Striding: $x$에서 윈도우를 한 번만 이동시키는 것 대신에, 한 번에 두 세번씩 더 큰 스텝을 진행할 수 있다. 예시: 입력 $x$가 1차원이고 크기가 100이며, $w$의 크기가 5라고 가정하자. 위 표는 스텝이 1 또는 2인 출력 크기를 보여주고 있다.
-
패딩: 보통 심층 신경망Deep Neural Networks 아키텍처를 설계할 때, 입력의 양 끝단에 0으로 채워주는(일반적으로 0, 0이 아닐 수도 있음) 패딩을 해줌으로써 합성곱의 출력을 입력과 같은 크기로 만들어준다. 주로 패딩은 우리의 편의를 위해 사용하는 것이며, 때로는 성능에 영향을 주고, 이상한 Border Effect를 가져올 수 있다. 즉, ReLU 비선형성을 사용할 때에는 제로 패딩Zero padding을 사용하는 것은 괜찮은 방법이다.
심층 합성곱 신경망 (DCNNs: Deep Convolution Neural Networks)
앞서 기술한 바와 같이, 일반적으로 심층 신경망은 선형 연산자와 점별수렴 비선형 계층 사이에 반복 교대로 구성된다. 합성곱 신경망에서 선형 연산자는 앞서 말한 합성곱 연산자가 될 것이다. 풀링Pooling 계층라고 불리는 세 번째 옵션도 있다.
이렇게 계층을 여러 겹 쌓는 이유는 데이터의 계층적 표현을 만들고자 하기 때문이다. 기술적으로 CNN은 배열의 형태를 가진 어떠한 유형의 데이터에도 적용될 수 있다. 즉, CNN은 이미지 및 영상 처리에만 국한되지 않고, 음성와 언어 처리에도 성공적으로 응용되고 있다.
왜 우리는 이 세상을 위계적, 계층적으로 표현Hierarchical representation하려 하는가? 그 이유는 우리가 살고 있는 세상이 구성적Compositional이기 때문이라는 것을 이전 절에서 언급한 바가 있다. 국소 픽셀이 모여 지향적인 윤곽선Edge, 또는 경계선 같은 단순한 모티브를 만들어 낸다는 점에서 이러한 계층적 성질을 관찰할 수 있다. 이 윤곽선들은 훨씬 추상적인 모티브를 형성하기 위해 차례로 모여, 모서리나 T-교차점 등과 같은 국부적 특징을 형성한다. 이러한 계층적 표현을 계속해서 구축하며, 실제 우리가 현실 세계에서 관찰하는 대상을 만들어 낼 수 있다.

그림 10. ImageNet에 학습된 합성곱 신경망의 특징Feature [Zeiler & Fergus 2013]
자연 세계에서 관찰할 수 있는 이러한 구성적이고 계층적인 성질은, 시각적인 인식의 결과 뿐만 아니라 물리적 수준에서도 마찬가지로 적용된다. 가장 저수준으로 보면, 소입자가 모여 원자를 형성하고, 원자는 분자를 형성한다. 또한, 물리적으로 물질 및 물체의 일부, 완전한 물체를 형성하기 위해서는 이러한 과정을 계속 수행해야 한다.
이 세상의 구성적인 성질은 인간이 살고 있는 세계를 어떻게 이해하고 있는 지에 대한 아래의 아인슈타인의 수사적인 질문에 대한 답이 될 수 있을 것이다.
The most incomprehensible thing about the universe is that it is comprehensible.
“우주에 관해서 가장 이해할 수 없는 것은 그것이 이해 가능하다는 사실이다.”
아인슈타인 (A. Einstein)
얀 르쿤 교수님에게는 인간이 구성적인 성질로써 이 세상을 이해한다는 건 여전히 일종의 음모처럼 보인다. 그러나 얀 교수님은 저명한 미국의 수학자 Stuart Geman의 말을 인용하면서 구성성이 없다면 인간이 이 세계를 이해하는 데 어마어마한 마술이 필요할 것이라고 주장한다.
The world is compositional or God exists.
이 세상은 구성적이거나, 신이 존재한다.
미국의 수학자 스튜어트 게먼 (Stuart Geman)
생물학에서의 영감
그렇다면 왜 딥러닝을 연구함에 있어서 ‘이 세상은 이해할 수 있고, 구성적인 성질을 가지고 있다.’는 아이디어에 기반을 두어야 하는가? Simon Thorpe이 수행했던 연구로부터 이런 아이디어가 나왔다. 매 100ms마다 이미지 한 세트에 불빛을 비추고 피실험자들에게 이 이미지가 무엇인지 식별하라고 하였더니 알아 맞춘 실험으로, 우리가 일상에서 사물을 매우 빠르게 인식한다는 것을 보였다. 이 말은 즉슨, 사람이 물체를 감지하는 데 약 100ms 정도가 걸린다는 것이다. 아래 표는 뉴런이 한 영역에서 다음 영역으로 전파되는 데 걸리는 시간을 뇌 그림에 표기한 것이다.
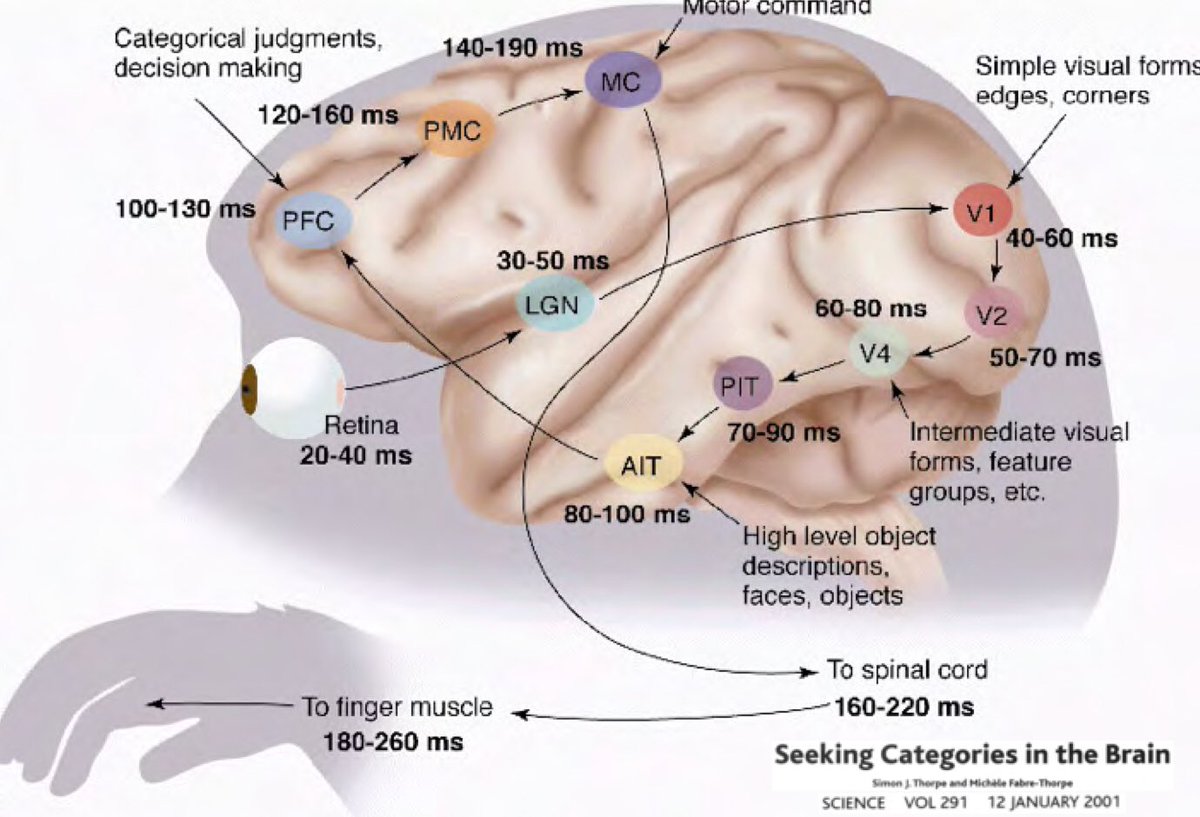
신호는 망막에서부터 대비향상Contrast Enhancement과 관문 조절Gate Control을 돕는 외측슬상핵(LGN)Lateral Geniculate Nucleus까지 전달되며, 그다음 일차시각피질V1 primary visual cortex, V2, V4, 그리고 뇌의 일부인 하측두 피질(PIT)Inferotemporal cortex로 전달된다. Open-brain 수술에서 관찰한 바에 따르면, 영화에서 어떤 배우를 보았을 때 하측두 피질에 있는 뉴런은 배우의 같이 특정 이미지를 감지할 때만 활동한다고 한다. 뉴런 활동은 위치, 크기, 조명, 배우가 서 있는 방향, 입고 있는 옷 등의 요소에 영향을 받지 않는다.
그러므로 인간이 사물을 인지하는 데에 걸리는 시간은 복잡하고 반복적인 계산에 시간을 쏟지 않고도 가능할 정도로 빠른 시간이라는 뜻이다. 정확히 말하자면, 이것은 하나의 피드포워드Feed-forward 과정이다.
이러한 발상은 입력의 변화에 무관하게 인지하지는 못하지만, 완전히 피드포워드로 구성되어 있는 신경망 아키텍처를 개발해 낼 수 있다는 것을 말해주었다.
Gallant와 Van Essen은 다음과 그림과 같이 사람의 두뇌는 두 가지 경로가 있다는 또 다른 발상을 해내었다.
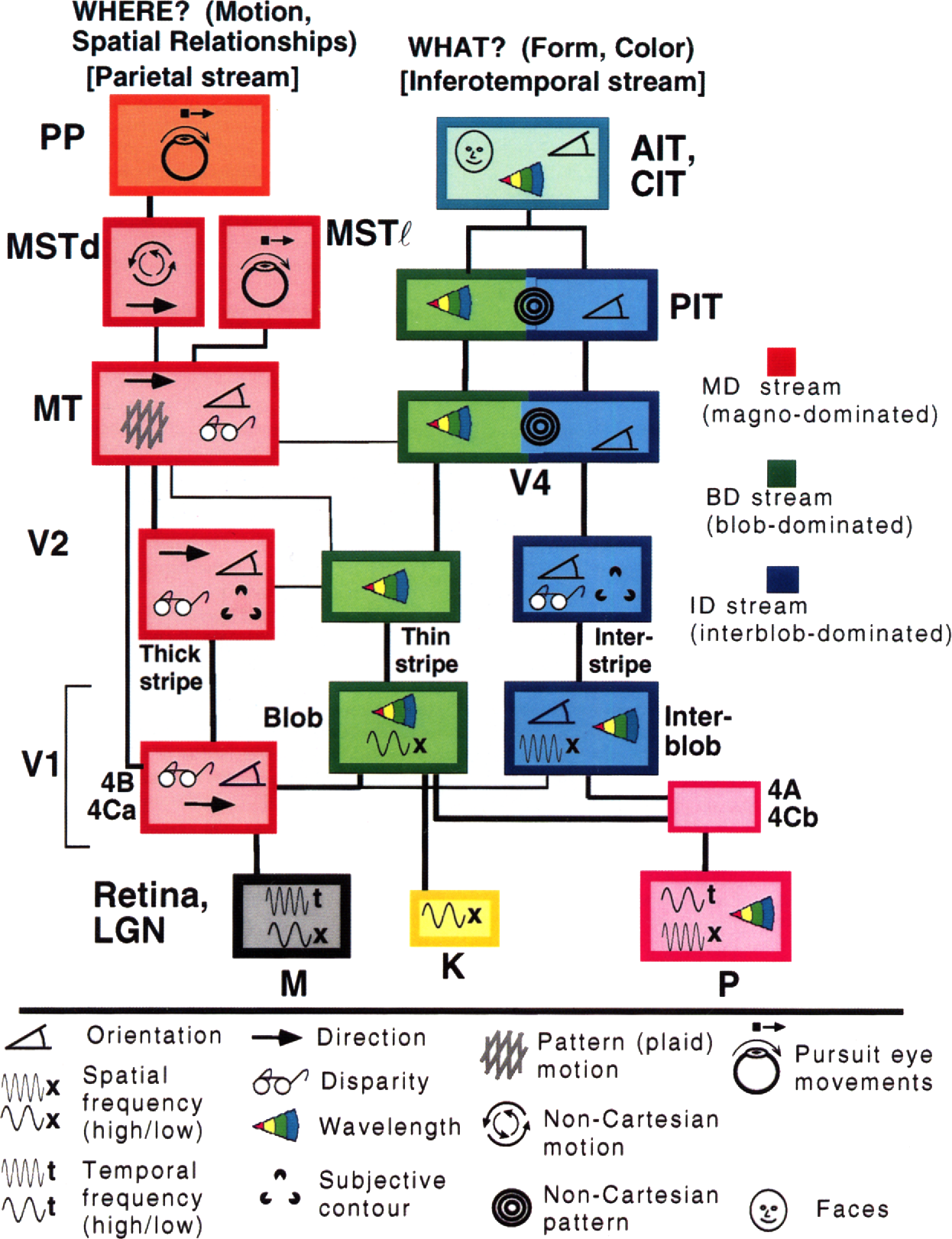
오른쪽은 배쪽경로Vental pathway로, 우리가 무엇을 보고 있는 지를 알려주고, 왼쪽은 등쪽경로Dorsal pathway로, 위치와 기하적인 구조, 동작을 식별한다. 이는 인간의 시각 피질Visual cortex 에서 완전히 분리되는 것처럼 보이지만 약간의 상호작용이 있긴 하다.
Hubel과 Weisel의 공헌 (1962)
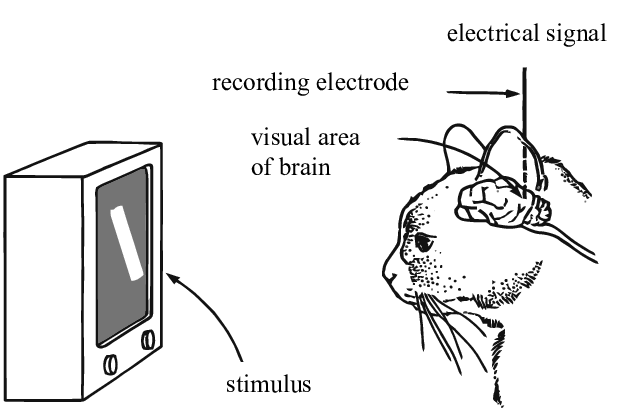
Hubel과 Weisel은 전극을 사용하여 시각적 자극에 대한 반응으로 고양이 두뇌에서의 뉴런 활동을 측정하는 실험을 하였다. 이 실험에서 V1 영역의 뉴런이 수용영역Receptive fields이라고 불리는 시야에서 특정 지역에서 민감하다는 것을 발견했다. 예를 들어, 고양이에게 세로 막대기를 보여주고 그 막대기를 회전시키면, 특정 각도에서 뉴런이 활동한다는 것을 증명했다. 비슷하게, 막대기가 그 각도에서 멀어질 수록 뉴런의 활성화 수치가 줄어들었다.
또한 만약 그 막대기를 시야 바깥으로 움직였을 때, 특정 뉴런이 활동을 멈추고 다른 뉴런이 활동하는 것을 발견하였다. 모든 시야에 상응하는 국부 피쳐 검출기Local feature detector가 존재하고, 인간의 두뇌가 여러 “합성곱” 으로 시각정 정보를 처리한다는 생각을 하게 되었다.
“복합 세포”Complex cells라고 불리는 또 다른 타입의 뉴런은 특정 영역 내에 여러 단순한 세포들의 출력을 종합하는 역할을 한다. 우리는 이러한 복합세포들이 최대값Maximum, 합산Sum, 제곱합Sum of squares과 같은 순서에 구애받지 않는 함수들을 사용하여 값을 집계하고 활성화 해주는 역할을 해낸다고 생각할 수 있다. 이런 복합 세포들은 자극이 영역 내에 어디에 위치하는 지에 상관 없이 그 영역의 엣지와 방향을 검출해낸다. 다시 말해, 입력의 위치가 조그만 변화에 대해서 이동불변Shift-invariant하다고 한다.
후쿠시마 박사의 공헌 (1982)
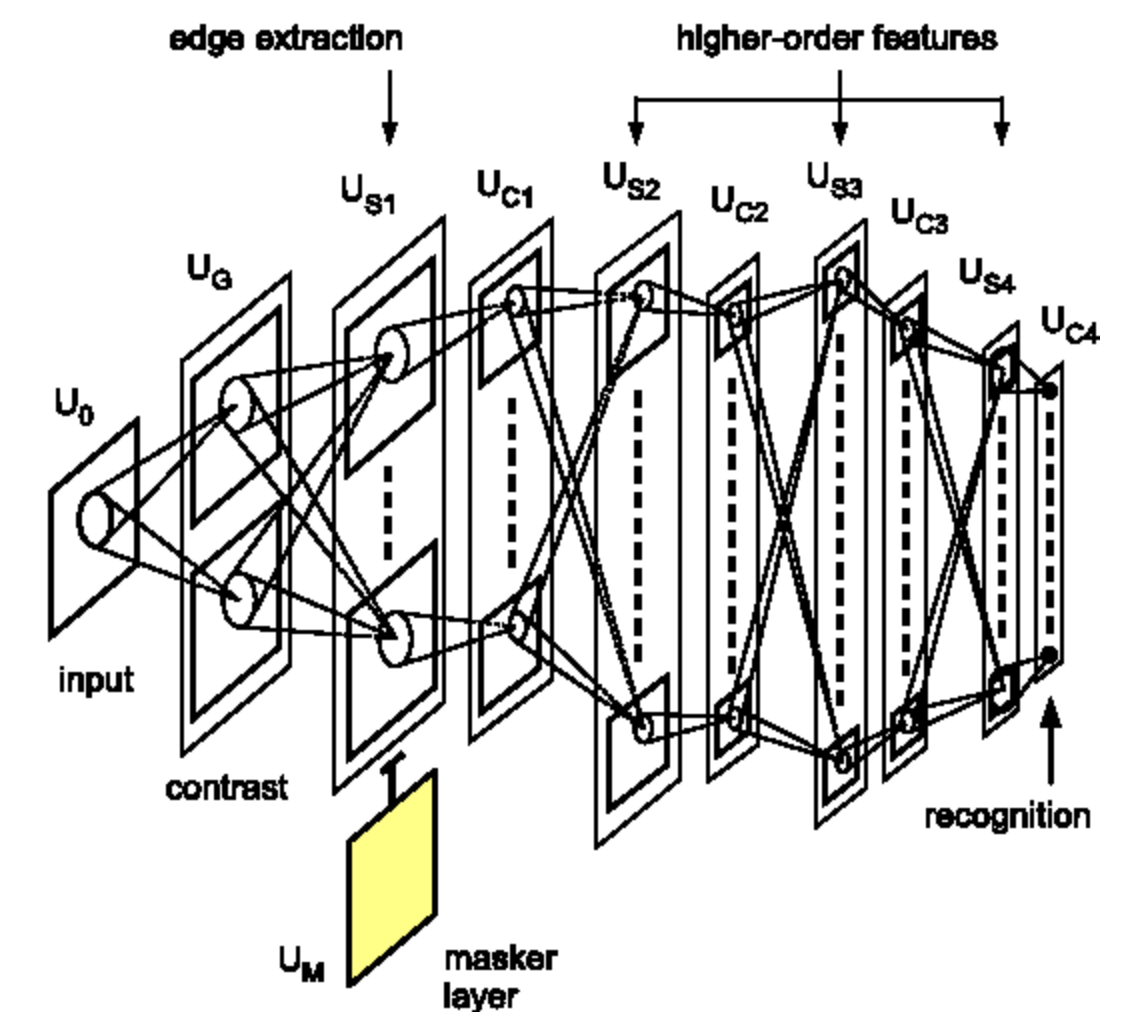
후쿠시마 박사는 수기로 작성한 숫자 데이터 셋으로 여러 레이어의 단일 세포와 복합 세포 모델을 컴퓨터로 처음 구현한 사람이다. 몇몇 피쳐 검출기들은 수작업으로 만들어지거나, 비지도 군집화Unsupervised clustering 알고리즘을 사용하여 학습되었다. 물론 역전파는 아직 사용되지 않았기 때문에 각 레이어마다 따로 학습되었다.
얀 르쿤 교수님은 몇 년 뒤에(1989, 1998) 같은 아키텍쳐를 구현하였지만 역전파를 이용한 지도학습으로 학습시켰고, 이 방식이 현대 합성곱 신경망의 기원으로 널리 알려지게 되었다. (MIT의 Riesenhuber 역시도 1999년에 이 아키텍쳐를 다시 고안해내었지만, 역전파를 사용하지는 않았다.)
Leave a comment